⎯⎯ ୨ Fodder ୧ ⎯⎯

1. Let p stand for the proposition “I plant a seed in the garden” and q for “A plant grows in the garden”. Express the following proposition as natural English sentences.
   a) $¬p$ = “I didn’t plant a see in the garden”
   b) $p \vee q$ = “I plant a seed in the garden or a plant grows in the garden”
   c) $p \wedge q$ = “I plant a seed in the garden and a plant grows in the garden”
   d) $p \Rightarrow q$ = “I plant a seed in the garden, therefore, a plant should grow in the garden”
   e) $¬p \vee q$ = “I did’t plant a seed in the garden or a plant grows in the garden”
   f) $¬p \Rightarrow ¬q$ = “I didn’t plant a seed in the garden, therefore, a plant shouldn’t grow in the garden”
   g) $¬p \vee (p \wedge q)$ = “I didn’t plant a seed in the garden or I plant a seed in the garden and a plant grows in the garden.

2. Show that the propositions $ p \Rightarrow q$ and $¬p \vee (p \wedge q) $ have the same truth values, not matter what the truth values of p and q are.

p	q	$¬p \vee (p \wedge q)$	$p \Rightarrow q$
T	T	T	T
T	F	F	F
F	T	T	T
F	F	T	T

Explaining the results of $¬p \vee (p \wedge q)$:

$¬p \vee (p \wedge q) \Rightarrow$ not p or (p and q)

Case 1: P and Q are True
not p or (p and q)
$\Leftrightarrow$ not True or (True and True)
$\Leftrightarrow$ False or True
$\Leftrightarrow$ True

Case 2: P is True and Q is False
not p or (p and q)
$\Leftrightarrow$ not True or (True and False)
$\Leftrightarrow$ False or False
$\Leftrightarrow$ False

Case 3: P is False and Q is True
not p or (p and q)
$\Leftrightarrow$ not False or (False and True)
$\Leftrightarrow$ True or False
$\Leftrightarrow$ True

Case 4: P and Q are True not p or (p and q)
$\Leftrightarrow$ Not False or (False and False)
$\Leftrightarrow$ True or False
$\Leftrightarrow$ True

$ \therefore ¬p \vee (p \wedge q) \Leftrightarrow p \Rightarrow q $

3. Let A be the set of real numbers R. Express the following proposition with a simple sentence.
   ∀ x ∈ A, ∃ y ∈ A [(x < y) ∧ (∀ z ∈ A (x < z) ⇒ (y ≤ z))]
   Is this proposition TRUE ? If not, is there a set A for which it is TRUE? Justify your answer.

For every real number, x, there exists a real number that is larger than x, y, and for every real number that is larger than x is also larger than y. The proposition is only true when z is larger than y but the scope of the proposition allows for y to be larger than z making it false.

If set $A = [n_1, n_2,], n_1, n_2 ∈ Z \text{ and } n_2 \neq n_1 $ then the statement would be true. This would allow x to equal the smallest number in A and y and z would have to both equal the largest number in A, making them equal and satisfying the proposition.

4. Let A = [0, 1]. Let x ∈ R and P(x) be the proposition (∀ a ∈ A, a ≤ x) ∧ (∀ b ∈ R, (∀ a ∈ A, a ≤ b) ⇒ x ≤ b) For which x is P(x) TRUE? Justify your answer

The first half of the statement (∀ a ∈ A, a ≤ x) implies that 1 ≤ x (1 being the highest value a can be)
The second half of the statement (∀ b ∈ R, (∀ a ∈ A, a ≤ b) ⇒ x ≤ b) implies that 1 ≤ b and x ≤ b, therefore x ≤ 1 because x must must be smaller then b and the smallest b could be is 1.
Having both statements of x ≤ 1 and 1 ≤ x implies that x = 1 for the initial statement to be true.

---

---

---

1. [2 points each]

(a) Let $\vec{u} = (1, 2, 3), \vec{v} = (3, 5, 1), \vec{w} = (0, 0, 8) \in \mathbb{R}^3$. Is (2, 3, −6) a linear combination of $\vec{u}, \vec{v}, \vec{w}$?

Let $\vec{a} = (2, 3, −6)$

$ \vec{a} = c_1 \left(\begin{array}{r} 1,& \\ 2,& \\ 3& \end{array}\right) + \ c_2 \left(\begin{array}{r} 3,& \\ 5,& \\ 1& \end{array}\right) + \ c_3 \left(\begin{array}{r} 0,& \\ 0,& \\ 8& \end{array}\right) $

$ \Leftrightarrow \left(\begin{array}{rrrrrrrrrrr} c_1 \cdot 1 + c_2 \cdot 3 + c_3 \cdot 0 \\ c_1 \cdot 2 + c_2 \cdot 5 + c_3 \cdot 0 \\ c_1 \cdot 3 + c_2 \cdot 1 + c_3 \cdot 8 \end{array}\right) $$

$ \Leftrightarrow \left(\begin{array}{rrrrrrrrrrr} c_1 + 3c_2 \\ 2c_1 + 5c_2 \\ 3c_1 + c_2 + 8c_3 \end{array}\right) $

$ \Leftrightarrow \left(\begin{array}{rrrrrrrrrrr} 2 = c_1 + 3c_2 \\ 3 = 2c_1 + 5c_2 \\ -6 = 3c_1 + c_2 + 8c_3 \end{array}\right) $

$ \Leftrightarrow \left(\begin{array}{rrrrrrrrrrr} c_1 = 2 - 3c_2 \\ c_2 = \frac{3}{5} - \frac{2}{5}c_1 \\ c_3 = - \frac{3}{4} - \frac{3}{8}c_1 - \frac{1}{8}c_2 \end{array}\right) $

$c_1 = 2 - 3c_2$
$ \Rightarrow c_1 = 2 - 3(\frac{3}{5} - \frac{2}{5}c_1)$
$ \Rightarrow c_1 = 2 - \frac{9}{5} + \frac{6}{5}c_1$
$ \Rightarrow - \frac{1}{5}c_1 = \frac{1}{5}$
$ \Rightarrow c_1 = -1$

$c_2 = \frac{3}{5} - \frac{2}{5}c_1$
$ \Rightarrow c_2 = \frac{3}{5} - \frac{2}{5}(-1))$
$ \Rightarrow c_2 = \frac{3}{5} + \frac{2}{5}$
$ \Rightarrow c_2 = 1$

$c_3 = -\frac{3}{4} - \frac{3}{8}c_1 - \frac{1}{8}c_2$
$ \Rightarrow c_3 = - \frac{3}{4} - \frac{3}{8}(-1) - \frac{1}{8}(1)$
$ \Rightarrow c_3 = - \frac{3}{4} + \frac{3}{8} - \frac{1}{8}$
$ \Rightarrow c_3 = - \frac{1}{2}$

$\therefore (2, 3, −6)$ can be expressed as a linear combination; $(2, 3, −6) = - \vec{u} + \vec{v} - \frac{1}{2} \vec{w}$

(b) Let $\vec{u} = (3, k, −3), \vec{v} = (−2, 1, k + 1), \vec{w} = (1, k, −2) \in \mathbb{R}^3$. Find the values of $ k \in \mathbb{R}$ such that $\vec{u} \cdot (\vec{v} + \vec{w}) = 0$.

$\vec{u} \cdot (\vec{v} + \vec{w}) = 0 \Rightarrow 0 = u_1(v_1 + w_1) + u_2(v_2 + w_2) + u_3(v_3 + w_3)$
$\Rightarrow 0 = 3((-2) + 1) + k(1 + k) - 3((k + 1) + (-2))$
$\Rightarrow 0 = 3(-1) + k(1 + k) - 3(k - 1)$
$\Rightarrow 0 = - 3 + k + k^2 - 3k + 3$
$\Rightarrow 0 = k^2 - 2k$
$\Rightarrow 0 = k(k - 2)$

$ \therefore k = \lbrace 0, 2 \rbrace$ such that $\vec{u} \cdot (\vec{v} + \vec{w}) = 0 $

(c) Let $\vec{e_1} = (1, 0, 0), \vec{e_2} = (0, 1, 0), \vec{e_3} = (0, 0, 1) \in \mathbb{R}^3$. Find all real numbers $c \in \mathbb{R}$ such that the angle between the vectors $2 \vec{e_1} + 2 \vec{e_2} + ( c − 2 ) \vec{e_3}$ and $2e_1 +(c−2)e_2 +2e_3$ is $\pi/3$.

Let $ a = 2 \vec{e_1} + 2 \vec{e_2} + ( c − 2 ) \vec{e_3}$
Let $ b = 2e_1 +(c−2)e_2 +2e_3$

Use Angel Theorem to apply $\theta$ where $\theta$ is the angel between $ \vec{a}$ and $ \vec{b} $:
$ \vec{a} \circ \vec{b} = || \vec{a} |||| \vec{b} || \cos \theta $

First, find $ \vec{a} \circ \vec{b}$ and $|| \vec{a} |||| \vec{b} ||$
$ \vec{a} \circ \vec{b} = (2 \vec{e_1} + 2 \vec{e_2} + ( c − 2 ) \vec{e_3}) \circ (2e_1 +(c−2)e_2 +2e_3)$ $ \Rightarrow (2(1, 0, 0) + 2(0, 1, 0) + ( c − 2 )(0, 0, 1)) \circ (2(1, 0, 0) +(c−2)(0, 1, 0) +2(0, 0, 1))$ $ \Rightarrow ((2, 0, 0) + (0, 2, 0) + (0, 0, c - 2)) \circ ((2, 0, 0) + (0, c - 2, 0) + (0, 0, 2))$
$ \Rightarrow (2, 2, c - 2) \circ (2, c - 2, 2)$
$ \Rightarrow 4 + 2c - 4 + 2c - 4$
$ \Rightarrow 4c - 4$

$|| \vec{a} |||| \vec{b}|| = (\sqrt{\vec{a} \circ \vec{a}}) ( \sqrt{ \vec{b} \circ \vec{b}})$
$ \Rightarrow ((\sqrt{(2, 2, c-2) \circ (2, 2, c-2)}) ( \sqrt{ (2, c-2, 2) \circ (2, c-2, 2)})$ *sub in simplified a and b
$ \Rightarrow ((\sqrt{ 4 + 4 + (c^2 - 4c + 4)}) ( \sqrt{(4 + (c^2 - 4c + 4) + 4)})$
$ \Rightarrow c^2 - 4c + 12$

$ \vec{a} \circ \vec{b} = || \vec{a} |||| \vec{b} || \cos \theta $
$ \Rightarrow 4c - 4 = (c^2 - 4c + 12) \cos \theta $
$ \Rightarrow 4c - 4 = (c^2 - 4c + 12)(0.5) $
$ \Rightarrow 8c - 8 = (c^2 - 4c + 12) $
$ \Rightarrow 0 = c^2 - 12c + 20 $ $ \Rightarrow 0 = (c - 10)(c - 2) $

$ \therefore c = \lbrace 2, 10 \rbrace $ such that the angle between the vectors $2 \vec{e_1} + 2 \vec{e_2} + ( c − 2 ) \vec{e_3}$ and $2e_1 +(c−2)e_2 +2e_3$ is $\pi/3$.

(d) Show that there are no vectors $\vec{u}, \vec{v} \in \mathbb{R}^n$ such that $|| \vec{u} || = 1, || \vec{v} || = 2 $ and $ \vec{u} \cdot \vec{v} = 3 $.

Use Angel Theorem to apply all statements into a single statement, and if the new statement is false then $\vec{u}$ and $\vec{v}$ cannot exist with the conditions listed.

$ \vec{u} \circ \vec{v} = || \vec{u} |||| \vec{v} || \cos \theta $
$ \Rightarrow (3) = (1)(2) \cos \theta $
$ \Rightarrow 3 = 2 [-1, 1] $
there is no value of $ \cos \theta$ that could multiply 2 into 3 (at most it would be 2)

$ \therefore \vec{u}$ and $\vec{v}$ cannot be real vectors under the listed conditions.

2. [4 points each] Let $ \vec{u}, \vec{v} \in \mathbb{R}^n$ be vectors in Rn

(a) Show that $4 \vec{u} \circ \vec{v} = || \vec{u} + \vec{v} ||^2 − || \vec{u} − \vec{v} ||^2.$ Show that $\vec{u}$ and $\vec{v}$ is orthogonal if and only if $|| \vec{u} + \vec{v} || = || \vec{u} − \vec{v} ||$.

$ || \vec{u} + \vec{v} ||^2 − || \vec{u} − \vec{v} ||^2$
$ \Rightarrow \sqrt{( \vec{u} + \vec{v} ) \circ ( \vec{u} + \vec{v} )}^2 − \sqrt{( \vec{u} - \vec{v} ) \circ ( \vec{u} - \vec{v} )}^2$
$ \Rightarrow ( \vec{u} + \vec{v} ) \circ ( \vec{u} + \vec{v} ) − ( \vec{u} - \vec{v} ) \circ ( \vec{u} - \vec{v} )$
$ \Rightarrow ( \vec{u} \circ \vec{u} + 2 \vec{u} \circ \vec{v} + \vec{v} \circ \vec{v} ) − ( \vec{u} \circ \vec{u} - 2 \vec{u} \circ \vec{v} + \vec{v} \circ \vec{v} )$ $ \Rightarrow \vec{u} \circ \vec{u} + 2 \vec{u} \circ \vec{v} + \vec{v} \circ \vec{v} − \vec{u} \circ \vec{u} + 2 \vec{u} \circ \vec{v} - \vec{v} \circ \vec{v}$
$ \Rightarrow 4 \vec{u} \circ \vec{v}$

$ \therefore 4 \vec{u} \circ \vec{v} = || \vec{u} + \vec{v} ||^2 − || \vec{u} − \vec{v} ||^2$

$|| \vec{u} + \vec{v} ||$.
$ \Rightarrow \sqrt{( \vec{u} + \vec{v} ) \circ ( \vec{u} + \vec{v} )}$
$ \Rightarrow \sqrt{ \vec{u} \circ \vec{u} + 2 \vec{u} \circ \vec{v} + \vec{v} \circ \vec{v}}$
$ \Rightarrow \sqrt{ \vec{u} \circ \vec{u} + \vec{v} \circ \vec{v}}$ (assuming $ \vec{u} \circ \vec{v} = 0 $)

$|| \vec{u} - \vec{v} ||$.
$ \Rightarrow \sqrt{( \vec{u} - \vec{v} ) \circ ( \vec{u} - \vec{v} )}$
$ \Rightarrow \sqrt{ \vec{u} \circ \vec{u} - 2 \vec{u} \circ \vec{v} + \vec{v} \circ \vec{v}}$
$ \Rightarrow \sqrt{ \vec{u} \circ \vec{u} + \vec{v} \circ \vec{v}}$ (assuming $ \vec{u} \circ \vec{v} = 0 $)

$ \therefore || \vec{u} + \vec{v} || = || \vec{u} − \vec{v} ||$ is true only if $ \vec{u} \circ \vec{u} = 0$; $\vec{u}$ and $\vec{v}$ are orthogonal

(b) State and prove the Cauchy–Schwarz inequality. Give a necessary and sufficient condition on $\vec{u}, \vec{v} \in \mathbb{R}^n$ such that the equality holds

The Cauchy-Schwarz inequality is $ | \vec{u} \circ \vec{v} | \leq || \vec{u} |||| \vec{v} || $

$ || \vec{u} + t \vec{v} || \geq 0, t \in \mathbb{R} $
$ \Rightarrow \sqrt{(\vec{u} + t \vec{v}) \circ ( \vec{u} + t \vec{v})} \geq 0 $
$ \Rightarrow (\vec{u} + t \vec{v}) \circ ( \vec{u} + t \vec{v}) \geq 0 $
$ \Rightarrow \vec{u}^2 + t^2 || \vec{v}^2 || + 2t( \vec{u} + \vec{v}) \geq 0 $ \

We can rewrite the above function as a discrete function where: $a = (\vec{u} \circ \vec{u}), b = (2 \vec{u} \vec{v}), c = (\vec{v} \circ \vec{v})$

$ b^2 - 4ac \leq 0 $
$ \Rightarrow (2 \vec{u} \circ \vec{v})^2 - 4(\vec{u} \circ \vec{u})(\vec{v} \circ \vec{v} \leq 0$
$ \Rightarrow (2 \vec{u} \circ \vec{v})^2 - 4(||\vec{u}^2||)(||\vec{v}^2||) \leq 0$
$ \Rightarrow (2 \vec{u} \circ \vec{v})^2 \leq 4(||\vec{u}^2||)(||\vec{v}^2||) $
$ \Rightarrow 2 \vec{u} \circ \vec{v} \leq 2||\vec{u}||||\vec{v}|| $
$ \Rightarrow \vec{u} \circ \vec{v} \leq ||\vec{u}||||\vec{v}|| $
$ \Rightarrow | \vec{u} \circ \vec{v} | \leq ||\vec{u}||||\vec{v}|| , \vec{u} \circ \vec{v} \geq 0 $
$ \Rightarrow | \vec{u} \circ \vec{v} | = ||\vec{u}||||\vec{v}|| $

$ \therefore \vec{u} \circ \vec{v} \leq ||\vec{u}||||\vec{v}|| $

The equality holds when $\vec{u}$ and $\vec{v}$ are scaler multiples of each other
$| \vec{u} \circ \vec{v} | \leq || \vec{u} |||| \vec{v} || $
$\Rightarrow | \vec{u} \circ c \vec{u} | \leq || \vec{u} |||| c \vec{u} || $ *since $\vec{v} = c \vec{u}, c \in \mathbb{R}, c > 0 $
$\Rightarrow | c(\vec{u} \circ \vec{u}) | \leq c|| \vec{u} |||| \vec{u} || $
$\Rightarrow | c(\vec{u} \circ \vec{u}) | \leq c (\vec{u} \circ \vec{u}) $
$ \Rightarrow -( c (\vec{u} \circ \vec{u})) \leq c(\vec{u} \circ \vec{u}) \leq c (\vec{u} \circ \vec{u}) $
$ \Rightarrow c(\vec{u} \circ \vec{u}) \leq c (\vec{u} \circ \vec{u}) $
$ \Rightarrow c(\vec{u} \circ \vec{u}) = c (\vec{u} \circ \vec{u}) $

(c) State and prove the triangle inequality. Assuming that both $\vec{u}$ and $\vec{v}$ are non-zero vectors, show that the equality holds if and only if $\vec{u}$ and $\vec{v}$ are parallel.

The Triangle inequality is $ || \vec{u} + \vec{v} || \leq || \vec{u} || + || \vec{v} || $ \

Start with the Cauchy Schwarz inequality:
$ | \vec{u} \circ \vec{v} | \leq || \vec{u} |||| \vec{v} || $
$ \Rightarrow -(|| \vec{u} |||| \vec{v}) || \leq \vec{u} \circ \vec{v} \leq || \vec{u} |||| \vec{v} || $
$ \Rightarrow \vec{u} \circ \vec{v} \leq || \vec{u} |||| \vec{v} || $
$ \Rightarrow 2 \vec{u} \circ \vec{v} \leq 2 || \vec{u} |||| \vec{v} || $
$ \Rightarrow || \vec{u} ||^2 + || \vec{v} ||^2 + 2 \vec{u} \circ \vec{v} \leq || \vec{u} ||^2 + || \vec{v} ||^2 + 2 || \vec{u} |||| \vec{v} || $ $ \Rightarrow \sqrt{|| \vec{u} ||^2 + || \vec{v} ||^2 + 2 \vec{u} \circ \vec{v}} \leq \sqrt{|| \vec{u} ||^2 + || \vec{v} ||^2 + 2 || \vec{u} |||| \vec{v} ||} $ $ \Rightarrow \sqrt{|| \vec{u} + \vec{v} ||^2} \leq \sqrt{(|| \vec{u} || + || \vec{v} ||)^2} $
$ \Rightarrow || \vec{u} + \vec{v} || \leq || \vec{u} || + || \vec{v} || $

$ \therefore $ The Triangle inequality is True because the Cauchy Schwarz inequality is True.

The equality holds when $\vec{u}$ and $\vec{v}$ are parallel
$|| \vec{u} + \vec{v} || \leq || \vec{u} || + || \vec{v} || $
$ \Rightarrow || \vec{u} + c \vec{u} || \leq || \vec{u} || + || c \vec{u} || $
$ \Rightarrow |( 1 + c )| || \vec{u} || \leq (1 + |c|) || \vec{u} || $
$ \Rightarrow |( 1 + c )| \leq (1 + |c|) $
$ \Rightarrow |( 1 + c )| = (1 + |c|) $

---

---

---

FILM 111 . Prompt 1. September 9 (due: Monday, Sept. 16)

The task in this assignment is to recognize and identify the various unusual or “experimental” cinematic techniques employed in Dziga Vertov’s Man with a Movie Camera (1929). The experimental cinematic techniques are those which significantly depart from straight, unaltered footage.

You may draw from this list: multiple exposures, fast motion, slow motion, freeze frames, close-ups, tracking shots, reversed footage, jump cuts, split screens, stop motion, etc.

Isolate two different segments of Man with a Movie Camera (roughly 60-120 seconds each). Each segment must be time stamped.

Provide a short paragraph (approx. 300 words) which identifies and briefly describes 3 techniques.

---

From 12:40 to 22:40, we are shown two distinct, experimental cinematic techniques. The first is a very unconventional tracking shot. At the beginning of the clip, the camera follows a small group of people in a carriage pulled by a horse. The next shot reveals that this footage was taken by the titular ‘man with a movie camera’ standing on the side door of a car - using his camera to balance himself - adjacent to the carriage. Although it is a very peculiar setup, he is using a moving camera to track a moving subject making it a tracking shot. The subsequent few shots show more tracking shots of people in carriages and of ’the man’ capturing those same shots. This continues until 22:15 where a shot of the horse hauling a carriage is paused and then a montage, the second cinematic technique, of freeze frames of various subjects and environments are displayed, the last of which in the film reel it was taken in. This is one of the frequent ways the film likes to remind its audience that every shot taken was captured in a camera and take them out of the film.

At 26:15 we see, presumably, a couple at a domestic relations court of some sort registering for a divorce. This is followed by a split shot, the third cinematic technique, of two shots traveling down a busy road. They are split vertically across the screen with the right shot tilted 45 degrees to the right and the left shot tilted 45 degrees to the left. This is likely to symbolize the couple going their separate ways with their different viewpoints on life.

And with that concludes 3 experimental cinematic techniques employed by Dziga Vertov’s “Man with a Movie Camera.”

---

---

---

1. Suppose $|x − 1| < \frac{1}{2}$. Show that: $| \frac{x}{1+x} -\frac{1}{2} | < \frac{|x - 1|}{3} $

---

$ |x − 1| < \frac{1}{2}$
$ \Rightarrow - \frac{1}{2} < x − 1 < \frac{1}{2}$
$ \Rightarrow \frac{1}{2} < x < \frac{3}{2}$
$ \therefore x \in (\frac{1}{2}, \frac{3}{2}) $

$$\begin{align} | \frac{x}{1+x} -\frac{1}{2} | < \frac{|x - 1|}{3} \\ | \frac{2x}{2(1+x)} -\frac{1 + x}{2(1 + x)} | < \frac{|x - 1|}{3} \\ | \frac{2x - 1 - x}{2(1+x)} | < \frac{|x - 1|}{3} \\ | \frac{x - 1}{2(1+x)} |< \frac{|x - 1|}{3} \\ \frac{1}{|2(1+x)|} < \frac{1}{3} \\ |2(1+x|) > 3 \\ |x + 1| > \frac{3}{2} \\ x + 1 > \frac{3}{2}, \text{*since x is always positive} \\ x > \frac{1}{2} \end{align}$$

$\therefore | \frac{x}{1+x} -\frac{1}{2} | < \frac{|x - 1|}{3} $

2. Write $ \lbrace x \in \mathbb{R} | (x − 1)(x + 1)(x + 2) < 0 \rbrace$ as a disjoint union of intervals.

first find critical points:
$ x -1 = 0 \Rightarrow x = 1$
$ x + 1 = 0 \Rightarrow x = -1$
$ x + 2 = 0 \Rightarrow x = -2$
These are the points where y switches signs, and we can use them to find the intervals where y is positive or negative.

1. $ (1, \infty), x = 100$
   $(x - 1)(x + 1)(x + 2)$
   $(100 - 1)(100 + 1)(100 + 2)$
   $(99))(101)(102)$
   $1019898$
   $1019898 > 0, \therefore (1, \infty)$ is not part of the set

2. $ (-1, 1), x = 0$
   $(x - 1)(x + 1)(x + 2)$
   $(0 - 1)(0 + 1)(0 + 2)$
   $(-1))(1)(2)$
   $-2$
   $-2 < 0, \therefore (-1, 1)$ is part of the set

3. $ (-2, -1), x = -1.5$
   $(x - 1)(x + 1)(x + 2)$
   $(-1.5 - 1)(-1.5 + 1)(-1.5 + 2)$
   $(-2.5)(-0.5)(0.5)$
   $0.625$
   $0.625 > 0, \therefore (-2, -1$ is not part of the set

4. $ (-\infty, -2), x = -100$
   $(x - 1)(x + 1)(x + 2)$
   $(-100 - 1)(-100 + 1)(-100 + 2)$
   $(-101))(-99)(-98)$
   $-979902$
   $-979902 < 0, \therefore (-\infty, -2)$ is part of the set

$ \therefore x$ can be expressed as $x = (-\infty, -2) \cup (-1, 1) $

3. Find the “natural domains” of:

a) $ f(x) = \sqrt{1 - \sqrt{4 - x^2}}$ \

the outermost square root requires: $ 1 - \sqrt{4 - x^2} \geq 0$
$\Rightarrow \sqrt{4 - x^2} \leq 1$
$\Rightarrow 4 - x^2 \leq 1$
$\Rightarrow x^2 \geq 3$
$\Rightarrow x \geq \sqrt{3} $
the innermost square root requires: $4 - x^2 \geq 0$,
$\Rightarrow x^2 \leq 4$
$\Rightarrow x \leq 2 $

$\therefore$ domain($f$) $= [\sqrt{3}, 2]$

b) $ g(x) = \sqrt{x - x^{-1}} \Rightarrow \sqrt{x - \frac{1}{x}} $

The square root requires: $x - \frac{1}{x} \geq 0$
$\Rightarrow \left(\begin{array}{rrrrrrrr} \text{if } x > 0, \text{ than } x^2 - 1 \geq 0 \\ \text{if } x < 0, \text{ than } x^2 - 1 \leq 0 \end{array}\right)$
$\Rightarrow \left(\begin{array}{rrrrrrrr} \text{if } x > 0, \text{ than } (x - 1)(x +1) \geq 0 \\ \text{if } x < 0, \text{ than } (x - 1)(x +1) \leq 0 \end{array}\right)$ \

$(x - 1)(x +1) \geq 0, x >0 \Rightarrow [1, \infty)$
$(x - 1)(x +1) \leq 0, x < 0 \Rightarrow [-1, 0]$

The relation $\frac{1}{x}$ implies: $ x \neq 0 $

$\therefore$ domain($f$) $= [-1, 0) \cup [1, \infty)$

c) $ h(x) = \sqrt{ \frac{\cos x}{\sin x}}$

The square root requires: $ \frac{\cos x}{\sin x} \geq 0 $
Therefore, any interval where $\cos{x}$ and $\sin{x}$ have the same signs should be in domain($h$). this is best solved for visually.

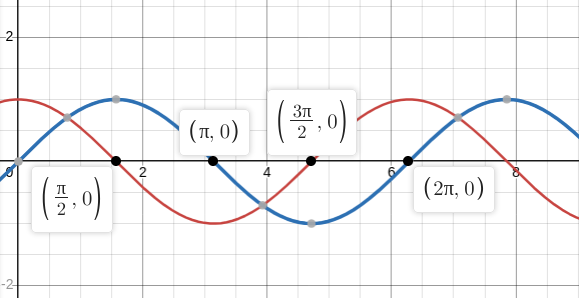
In this graph, the red line represents $\cos{x}$ and the blue line represents $\sin{x}$. You can see that both graphs are positive from 0 to $\frac{\pi}{2}$ and both are negative from $pi$ to $\frac{3\pi}{2}$.
$ \therefore$ domain($h$) $= (0, \frac{k\pi}{2}) \cup (k\pi, \frac{3k\pi}{2})$

4. Let $f (x) = \ln{(x + \sqrt{x^2 + 1})}$. What is the natural domain of $f$? Find a function $g$ such that $g \circ f (x) = x$ for all $x$ in the natural domain of $f$.

The square root requires: $ x^2 + 1 > 0 $
$ x^2 + 1 > 0, \forall x \in \mathbb{R}$, since x^2 + 1 is a upward facing parabola

The natural log requires: $ x + \sqrt{x^2 + 1} > 0 $
$ \Rightarrow \sqrt{x^2 + 1} > -x $
$ \Rightarrow x^2 + 1 > x^2 $

$ \therefore x + \sqrt{x^2 + 1} > 0, \forall x \in \mathbb{R} \Rightarrow$ domain($h$) $= \mathbb{R} $

Find g(x) such that $ g \circ f = x$ (aka: find the inverse of f(x)):
$g \circ f(x),$ Let $y = \ln{x + \sqrt{x^2 + 1}}$
$ \Rightarrow e^y = x + \sqrt{x^2 + 1}$
$ \Rightarrow e^y - x = \sqrt{x^2 + 1}$
$ \Rightarrow (e^y - x)^2 = x^2 + 1$
$ \Rightarrow (e^y)^2 - 2xe^y + x^2 = x^2 + 1$
$ \Rightarrow (e^y)^2 - 2xe^y = 1$
$ \Rightarrow (e^y)^2 - 1 = 2xe^y$
$ \Rightarrow \frac{(e^y)^2 - 1}{2e^y} = x$

$ \therefore g(x) = \frac{(e^x)^2 - 1}{2e^x}$

---

1. [2 points each]

(a) Show that $\vec{u}$ is orthogonal to $\vec{v} − Proj_{\vec{u}} \vec{v}$ for all vectors $\vec{u}, \vec{v} \in \mathbb{R}^n$ with $\vec{u} \neq 0$.

Sorry I couldn’t get all the questions done - I got food poisoning on the weekend

(b) Let $\vec{u} = (−4, 5, −2)$ and $\vec{v} = (−11, 4, −13)$. Find the projection $Proj_{\vec{u}} \vec{v}$. What is the length of$Proj_{\vec{u}} \vec{v}$.

$Proj_{\vec{u}} \vec{v} = \frac{ \vec{u} \circ \vec{v}}{|| \vec{u} ||} \vec{u}$
$\frac{ - 4(-11) + 5(4) - 2(-13)}{\sqrt{ -4(-4) + 5(5) - 2(-2) }} (-4, 5, -2)$
$\frac{44 + 20 + 26}{\sqrt{16 + 25 + 4}} (-4, 5, -2)$
$\frac{90}{\sqrt{45}} (-4, 5, -2)$
$\frac{30}{\sqrt{5}} (-4, 5, -2)$
$(\frac{-120}{\sqrt{5}}, \frac{150}{\sqrt{5}}, \frac{-60}{\sqrt{5}})$

$ \therefore$ the projection vector is $(\frac{-120}{\sqrt{5}}, \frac{150}{\sqrt{5}}, \frac{-60}{\sqrt{5}})$

$||(\frac{-120}{\sqrt{5}}, \frac{150}{\sqrt{5}}, \frac{-60}{\sqrt{5}}) ||$
$\sqrt{(\frac{-120}{\sqrt{5}}, \frac{150}{\sqrt{5}}, \frac{-60}{\sqrt{5}}) \circ (\frac{-120}{\sqrt{5}}, \frac{150}{\sqrt{5}}, \frac{-60}{\sqrt{5}})}$
$\sqrt{\frac{-120}{\sqrt{5}} \cdot \frac{-120}{\sqrt{5}} + \frac{150}{\sqrt{5}} \cdot \frac{150}{\sqrt{5}} + \frac{-60}{\sqrt{5}} \cdot \frac{-60}{\sqrt{5}}}$
$\sqrt{\frac{14400}{5} + \frac{22500}{5} + \frac{3600}{5}}$
$\sqrt{2880 + 4500 + 720}$
$\sqrt{8150}$
$5 \sqrt{326}$

$\therefore$ The length of the projection is $5 \sqrt{326}$

(c) Let $\vec{u} = (−2, 3, −1) \in \mathbb{R}^3$ and let $L$ be a line in $\mathbb{R}^3$ with a direction vector $\vec{d} = (−1, 1, 1)$. Find the projection $Proj_{L} \vec{u}$. What is the distance from $\vec{u}$ to $L$?

(d) Suppose that we have a plane in $\mathbb{R}^3$ given in the form $ax + by + cz + d = 0$ with $a, b, c, d \in \mathbb{R}$. Find a formula in terms of $a, b, c$ and $d$ for the distance from the plane to the origin $(0, 0, 0)$ in $\mathbb{R}^3$. Use the formula to find the distance from the point $B = (−1, 3, 4)$ to the plane $\rho : x + 4y − 6z + 8 = 0$.

(e) Find the cross products $\vec{u} \times \vec{v}$ and $\vec{v} \times \vec{u}$ where $\vec{u} = (2, 1, −2)$ and $\vec{v} = (−3, 4, 1)$. What does the cross product of $\vec{u}$ and $\vec{v}$ represent geometrically?

2. [2 points each]

(a) Find the equation of a plane through the points $P = (1, 1, 0), Q = (1, 0, 1)$ and $R = (0, 1, 2)$. Find the area of the triangle with vertices $P, Q, R$.

We can create the plane, $\delta$ with vectors made up of $P, Q, R$ to insure that it passes through them.

Let $ \vec{u} = Q - P = (0, -1, 1)$ Let $ \vec{v} = R - P = (-1, 0, 2)$

Vector form of $\delta$ is $ \delta = P + s \vec{u} + t \vec{v}$
$ \delta = (1, 1, 0) + s(0, -1, 1) + t(-1, 0, 2)$
$ \therefore $ the equation of the plane is $(1, 1, 0) + s(0, -1, 1) + t(-1, 0, 2)$ \

To find the area of the triangle whose vertices are $P, Q, R$, we can use $ || \vec{u} \times \vec{v}||$ because that will give use the area of the parallelogram with $\vec{v}$ and $\vec{u}$ which if halved should give us the area of the triangle.

$ || \vec{u} \times \vec{v} || $
$ || (0, -1, 1) \times (-1, 0, 2) || $
$ || ((-1(2) - 1(0)), (1(-1) - 0(2)), (0(0) - (-1)(-1))) || $
$ || ((-2), (-1), (-1)) || $
$ \sqrt{(-2, -1, -1) \times (-2, -1, -1)} $
$ \sqrt{((-2) \cdot (-2) + (-1) \cdot (-1) + (-1) \cdot (-1))} $
$ \sqrt{ 4 + 1 + 1} $
$ \sqrt{6} $
$ \therefore$ the area of the triangle $= \frac{\sqrt{6}}{2} $

(b) A plane passes through the point $(1, 2, −1)$, and is orthogonal to the line of intersection of thw two planes $2x + y + z = 2$ and $x + 2y + z = 3$. What is the equation of the plane?

First we find the intersection between the two planes.

Step 1: Convert the system into an augmented matrix $ \left[ \begin{array}{rrrrr} 2 & 1 & 1 & | & 2 \\ 1 & 2 & 1 & | & 3 \end{array} \right] $

Step 2: Put it into RREF:
$ R_1 - R_2, R_2 - R_1, $
$ \left[ \begin{array}{rrrrr} 1 & -1 & 0 & | & -1 \\ 0 & 3 & 1 & | & 4 \end{array} \right] $

$ R_2 \cdot \frac{1}{3} $
$ \left[ \begin{array}{rrrrr} 1 & -1 & 0 & | & -1 \\ 0 & 1 & \frac{1}{3} & | & \frac{4}{3} \end{array} \right] $

Step 3: Solve into line
$x - y = -1$
$y + z \frac{1}{3}= \frac{4}{3}$

$x = y - 1$
$y = t$
$z = 4 - 3y$

$ \left[ \begin{array}{r} x \\ y \\ z \end{array} \right] = \left[ \begin{array}{r} -1 \\ 0 \\ 4 \end{array} \right] + t \left[ \begin{array}{r} 1 \\ 1 \\ -3 \end{array} \right] $
or
(1, 1, -3)

The we use the orthogonal line and the point to make the plane.

$a(x - x_0) + b (y - y_0) + c (z - z_0) = 0$
$1(x - 1) + 1 (y - 2) + -3 (z - (-1)) = 0$
$x - 1 + y - 2 - 3z -3 = 0$
$x + y - 3z = 6$ \

$ \therefore x + y - 3z = 6$ is orthogonal to the give planes and hits the given point.

(c) Given two planes $x + 5y + z = 3$ and $x + 9y + 3z = 5$, find the line of intersection and the angle between the planes.

Step 1: Convert the system into an augmented matrix
$ \left[ \begin{array}{rrrrr} 1 & 5 & 1 & | & 3 \\ 1 & 9 & 3 & | & 5 \end{array} \right] $

Step 2: Convert matrix in RREF:
$ \left[ \begin{array}{rrrrr} 1 & 5 & 1 & | & 3 \\ 1 & 9 & 3 & | & 5 \end{array} \right] $

$ R_1 - R_2, R_1 \cdot \frac{-1}{4}$
$ \left[ \begin{array}{rrrrr} 0 & 1 & \frac{1}{2} & | & \frac{1}{2} \\ 1 & 9 & 3 & | & 5 \end{array} \right] $

$ R_2 - 9R_1$
$ \left[ \begin{array}{rrrrr} 0 & 1 & \frac{1}{2} & | & \frac{1}{2} \\ 1 & 0 & \frac{-3}{2} & | & \frac{1}{2} \end{array} \right] $

Step 3: Solve into line
$y + z \frac{1}{2} = \frac{1}{2}$
$x - z \frac{3}{2} = \frac{1}{2}$

$x = \frac{1}{2} + z \frac{3}{2}$
$y = \frac{1}{2} - z \frac{1}{2} $
$z = t$

$ \therefore \left[ \begin{array}{r} x \\ y \\ z \end{array} \right] = \left[ \begin{array}{r} \frac{1}{2} \\ \frac{1}{2} \\ 0 \end{array} \right] + t \left[ \begin{array}{r} \frac{3}{2} \\ \frac{-1}{2} \\ 1 \end{array} \right] $ is the line of intersection between the planes

To find the angle the planes intersect at, we can use the angle theorem with the normal vectors of each of the planes.

First, find the normal vectors of the planes

$\vec{n_1} = (1, 5, 1)$
$\vec{n_2} = (1, 9, 3)$

Then, we put the vectors into the angle theorem and solve for the angle.

$ \vec{n_1} \circ \vec{n_2} = || \vec{n_1} |||| \vec{n_2} || \cos \theta$, where $\theta$ is the angel between the two vectors
$ \cos^{-1} \frac{\vec{n_1} \circ \vec{n_2}}{|| \vec{n_1} |||| \vec{n_2} ||} = \theta$

$ \vec{n_1} \circ \vec{n_2}$
$ \Rightarrow (1, 5, 1) \circ (1, 9, 3) $
$ \Rightarrow 1 \cdot 1 + 5 \cdot 9 + 1 \cdot 3$
$ \Rightarrow 1 + 45 + 3$
$ \Rightarrow 49$

$|| (1, 5, 1) |||| (1, 9, 3) ||$
$ \Rightarrow \sqrt{(1, 5, 1) \circ (1, 5, 1)} \cdot \sqrt{(1, 9, 3) \circ (1, 9, 3)}$
$ \Rightarrow \sqrt{(1 \cdot 1 + 5 \cdot 5 + 1 \cdot 1)} \cdot \sqrt{(1 \cdot 1 + 9 \cdot 9 + 3 \cdot 3)}$
$ \Rightarrow \sqrt{(1 + 25 + 1)} \cdot \sqrt{(1 + 81 + 9)}$
$ \Rightarrow \sqrt{27} \cdot \sqrt{91}$ \

$ \cos^{-1} \frac{\vec{n_1} \circ \vec{n_2}}{|| \vec{n_1} |||| \vec{n_2} ||} = \theta$
$ \cos^{-1} \frac{49}{ \sqrt{27} \cdot \sqrt{91}} = \theta$
$ \cos^{-1} \frac{49}{ \sqrt{2457}} = \theta$
$ ~8.683159 = \theta$

$ \therefore$ the angle between the two planes is $ \cos^{-1} \frac{49}{\sqrt{2457}} $ or ~8.683159

(d) Find the equation of the set of all points that are equidistant from the points $P = (−2, 3, −1)$ and $Q = (5, 2, 4)$.

This set of points would be a plane perfectly between the two points, and oriented such that if the two points were made into a vector, it would be orthogonal.

To get this plane, we can use the two points to get a midpoint and a vector which we can use as a normal vector to get the equation of a plane.

$M = ( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}, \frac{z_1 + z_2}{2})$ where M is the midpoint
$M = ( \frac{-2 + 5}{2}, \frac{3 + 2}{2}, \frac{-1 + 4}{2})$
$M = ( \frac{3}{2}, \frac{5}{2}, \frac{3}{2})$

$ \vec{u} = \vec{PQ} = Q - P = ((5 - (-2)), (2 - 3), (4 - (-1))) = (7, -1, 5)$

$a(x - x_0) + b (y - y_0) + c (z - z_0) = 0$
$7(x - \frac{3}{2}) - 1(y - \frac{1}{2}) + 5(z - \frac{3}{2}) = 0$
$7x - \frac{21}{2} - y + \frac{1}{2} + 5z - \frac{15}{2} = 0$
$7x - y + 5z = \frac{35}{2}$

$ \therefore 7x - y + 5z = \frac{35}{2}$ is the equation of the set of points equidistant to $P$ and $Q$.

(e) Find the equation of the plane that contains the point $(1, 3, 0)$ and the line $L : x = 3 + 2t, y = −4t, z = 7 − t$ with $t \in \mathbb{R}$.

Let $R = (1, 3, 0)$

To make the plane, we can get two points from the line and use them with the given point to make a two vectors to get a normal vector which can then be used to make the plane.

Point 1: let $x = 5$
$ \Rightarrow 5 = 3 + 2t \Leftrightarrow t = 1$
$ y = -4t = -4(1) = -4$
$ z = 7 - t = 7 - 1 = 6$
$ \therefore P_1 = (5, -4, 6),$ where $P_1$ is a point on $L$

Point 2: let $z = 0$
$ \Rightarrow 0 = 7 - t \Leftrightarrow t = 7$
$ x = 3 + 2t = 3 + 2(7) = 17 $
$ y = -4t = -4(7) = -28 $
$ \therefore P_2 = (17, -28, 0),$ where $P_2$ is another point on $L$

Let $\vec{u} = \vec{RP_1} = P_1 - R = (4, -7, 6)$ Let $\vec{v} = \vec{RP_2} = P_2 - R = (16, -31, 0)$

$ \vec{u} \times \vec{v} = ((-7)(0) - (-31)(6), 6(16) - 0(4), 4(-31) - 16(-7)) = (186, 96, -16)$

$a(x - x_0) + b (y - y_0) + c (z - z_0) = 0$
$ \Leftrightarrow 186 (x - 1) + 96 (y - 3) - 16 (z - 0) = 0$
$ \Leftrightarrow 186x - 186 + 96y - 288 - 16z = 0$
$ \Leftrightarrow 186x + 96y - 16z = 474$ $ \Leftrightarrow 93x + 48y - 8z = 237$

$ \therefore 93x + 48y - 8z = 237$ is a plane that contains $L$ and the given point, R.

---

1. Find the following limits, if they exist. Justify your approach.

a) $ \lim\limits_{x \to 1} \frac{2 − \sqrt{x}}{x − 4} $

Step 1: Try Direct Substitution
$ \lim\limits_{x \to 1} \frac{2 − \sqrt{x}}{x − 4} = \frac{2 − \sqrt{1}}{1 − 4} = \frac{1}{− 3}$

$ \therefore \lim\limits_{x \to 1} \frac{2 − \sqrt{x}}{x − 4} = - \frac{1}{3} $

b) $ \lim\limits_{x \to 0} \frac{e^{2x} − 1}{e^x − 1} $

Step 1: Try Direct Substitution
$ \lim\limits_{x \to 0} \frac{e^{2x} − 1}{e^x − 1} = \frac{e^{2(0)} − 1}{e^{0} − 1} = \frac{1 − 1}{1 − 1} = \frac{0}{0}$

Step 2: Try L’Hopital’s Rule
$ \lim\limits_{x \to 0} \frac{2e^{2x}}{e^x} = \frac{2(e^x)^2}{e^x} = 2e^x $

Step 3: Try Direct Substitution with New Equation
$ \lim\limits_{x \to 0} 2e^x = 2e^0 = 0$

$\therefore \lim\limits_{x \to 0} \frac{e^{2x} − 1}{e^x − 1} = 0$

c) (bonus) $\lim\limits_{x→0} \frac{\sin{3x}}{x}$

Step 1: Try Direct Substitution
$\lim\limits_{x→0} \frac{\sin{3(0)}}{0} = \frac{0}{0}$

Step 2: Try L’Hopital’s Rule
$\lim\limits_{x→0} \frac{\sin{3x}}{x} = \frac{3 \cos{3x}}{1} = 3 \cos{3x}$

Step 3: Try Direct Substitution with New Equation $\lim\limits_{x→0} 3 \cos{3(0)} = 3 \cos{0} = 3 \times 1 = 3$

$\therefore \lim\limits_{x→0} \frac{\sin{3x}}{x} = 3$

2. Let $f (x) = \frac{|x|−x}{x} $. Find the following limits, if they exist.

a) $\lim\limits_{x \to 0^+} f (x)$

We can determine the limit from the right by substituting x with values bigger then x that get progressively closer to 0 so we can either corelate a pattern

$\lim\limits_{x \to 0^+} \frac{|1|−1}{1} = 0 $
$\lim\limits_{x \to 0^+} \frac{|0.1|−0.1}{0.1} = 0 $
$\lim\limits_{x \to 0^+} \frac{|0.01|−0.01}{0.01} = 0 $
$\lim\limits_{x \to 0^+} \frac{|0.001|−0.001}{0.001} = 0 $
$\lim\limits_{x \to 0^+} \frac{|0.0001|−0.0001}{0.0001} = 0 $

$ \therefore \lim\limits_{x \to 0^+} \frac{|x|−x}{x} = 0 $.

b) $\lim\limits_{x \to 0^-} f (x)$

Determine the limit from the left is the same process as the right; substituting values that are smaller than x and get progressively

$\lim\limits_{x \to 0^-} \frac{|-1|−(-1)}{-1} = -2 $
$\lim\limits_{x \to 0^-} \frac{|-0.1|−(-0.1)}{-0.1} = -2 $
$\lim\limits_{x \to 0^-} \frac{|-0.01|−(-0.01)}{-0.01} = -2 $
$\lim\limits_{x \to 0^-} \frac{|-0.001|−(-0.001)}{-0.001} = -2 $
$\lim\limits_{x \to 0^-} \frac{|-0.0001|−(-0.0001)}{-0.0001} = -2 $ \

$ \therefore \lim\limits_{x \to 0^-} \frac{|x|−x}{x} = -2$

c) $\lim\limits_{x \to 0} f (x)$

$ \lim\limits_{x \to 0^-} f(x) \neq \lim\limits_{x \to 0^+} f(x) $

$ \therefore \lim\limits_{x \to 0} f (x)$ dose not exists

3. Let the function: $$ f (x) = \left( \begin{array}{rrrrrrrrrrrrr} x^2 \text{ if} − 1 \leq x \le 0 \text{ or } 0 \le x \leq 1 \\ 1 \text{ if } x = 0 \\ 2x − 1 \text{ if } x \le −1 \text{ or } x \ge 1 \end{array} \right) $$

a) Sketch the graph of $f$

• graph!!

b) Discuss the continuity of $f$ at $x = −1, 1, 0$.

-1: There is a jump discontinuity at -1 because although $\lim\limits_{x \to -1^-} f(x)$ and $\lim\limits_{x \to -1^+} f(x)$ exist judging from the graph, they are not equal.

0: There is a removal discontinuity at 0 because the limits from both sides exist and are equal, but $\lim\limits_{x \to 0} f(x) \neq f(0)$

1: the function is continuous at 1 because the limits at both sides exist, are equal and equal to the function at 1.

4. Let the functions $f (x) = \sqrt{x} − 2, g(x) = x^2, h(x) = x^3 + 2$. Write the composite function $f \circ g \circ h$ and give its natural domain.

$ f \circ g \circ h = f(g(h(x)))$
$ = f(g(x^3 + 2)) = f((x^3 + 2)^2) = \sqrt{(x^3 + 2)^2} - 2$
$ = x^3 + 2 - 2 = x^3$

$ \therefore f \circ g \circ h = x^3$

there isn’t anything about $x$ or $x^3$ that needs a restriction of the domain.
$\therefore$ domain($ f \circ g \circ h$) = $ \mathbb{R} $

---

1. [2 pts] List the different types of RREF possible for a $2 \times 4$ matrix.

From my research, there isn’t different types of RREF, so i am going to make my own arbitrary types. From my findings, three distinct catagories emerged based on the amount of independent variables in the matrix

1. No Independent Variables - 1 matrix

$ \left[ \begin{array}{rrr} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right] $

2. One Independent Variables - 4 matrixes

Let $ n \in \mathbb{R} $

$ \left[ \begin{array}{rrr} 1 & n & n & n \\ 0 & 0 & 0 & 0 \end{array} \right] $

$ \left[ \begin{array}{rrr} 0 & 1 & n & n \\ 0 & 0 & 0 & 0 \end{array} \right] $

$ \left[ \begin{array}{rrr} 0 & 0 & 1 & n \\ 0 & 0 & 0 & 0 \end{array} \right] $

$ \left[ \begin{array}{rrr} 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{array} \right] $

3. Two independent Variables - 6

Let $ n \in \mathbb{R} $

$ \left[ \begin{array}{rrr} 1 & n & n & n \\ 0 & 1 & n & n \end{array} \right] $

$ \left[ \begin{array}{rrr} 1 & n & n & n \\ 0 & 0 & 1 & n \end{array} \right] $

$ \left[ \begin{array}{rrr} 1 & n & n & n \\ 0 & 0 & 0 & 1 \end{array} \right] $

$ \left[ \begin{array}{rrr} 0 & 1 & n & n \\ 0 & 0 & 1 & n \end{array} \right] $

$ \left[ \begin{array}{rrr} 0 & 1 & n & n \\ 0 & 0 & 0 & 1 \end{array} \right] $

$ \left[ \begin{array}{rrr} 0 & 0 & 1 & n \\ 0 & 0 & 0 & 1 \end{array} \right] $

2. [1 pt each] Put the following matrices into RREF.

$$ (a) \left[ \begin{array}{rrr} 3 & 2 & 1 \\ 6 & 5 & 4 \end{array} \right] $$

$$ \left[ \begin{array}{rrr} 3 & 2 & 1 \\ 6 & 5 & 4 \end{array} \right] \overrightarrow{R_2 - 2R_1} \left[ \begin{array}{rrr} 3 & 2 & 1 \\ 0 & 1 & 2 \end{array} \right] \overrightarrow{R_1 \cdot \frac{1}{3}} \left[ \begin{array}{rrr} 1 & \frac{2}{3} & \frac{1}{3} \\ 0 & 1 & 2 \end{array} \right] $$

$$ (b) \left[ \begin{array}{rrr} 10 & 6 & 9 \\ 15 & 9 & 12 \end{array} \right] $$

$$ \left[ \begin{array}{rrr} 10 & 6 & 9 \\ 15 & 9 & 12 \end{array} \right] \overrightarrow{ R_2 \cdot \frac{1}{3}} \left[ \begin{array}{rrr} 10 & 6 & 9 \\ 5 & 3 & 4 \end{array} \right] \overrightarrow{ R_1 - 2R_2} \left[ \begin{array}{rrr} 0 & 0 & 1 \\ 5 & 3 & 4 \end{array} \right] $$

$$ \left[ \begin{array}{rrr} 0 & 0 & 1 \\ 5 & 3 & 4 \end{array} \right] \overrightarrow{ R_2 \cdot \frac{1}{5}} \left[ \begin{array}{rrr} 0 & 0 & 1 \\ 1 & \frac{3}{5} & \frac{4}{5} \end{array} \right] \overrightarrow{ R_1 \leftrightarrow R_2} \left[ \begin{array}{rrr} 1 & \frac{3}{5} & \frac{4}{5} \\ 0 & 0 & 1 \end{array} \right] $$

$$ (c) \left[ \begin{array}{rrrr} 2 & -6 & -1 & 6 \\ 4 & -12 & 2 & 20 \\ 3 & -9 & 0 & 12 \end{array} \right] $$

$$ \left[ \begin{array}{rrrr} 2 & -6 & -1 & 6 \\ 4 & -12 & 2 & 20 \\ 3 & -9 & 0 & 12 \end{array} \right] \overrightarrow{R_2 - 2R_1} \left[ \begin{array}{rrrr} 2 & -6 & -1 & 6 \\ 0 & 0 & 4 & 8 \\ 3 & -9 & 0 & 12 \end{array} \right] \overrightarrow{R_3 - R_1} \left[ \begin{array}{rrrr} 2 & -6 & -1 & 6 \\ 0 & 0 & 4 & 8 \\ 1 & 3 & 1 & 6 \end{array} \right] $$

$$ \left[ \begin{array}{rrrr} 2 & -6 & -1 & 6 \\ 0 & 0 & 4 & 8 \\ 1 & 3 & 1 & 6 \end{array} \right] \overrightarrow{R_1 - 2R_3} \left[ \begin{array}{rrrr} 0 & -12 & -3 & -6 \\ 0 & 0 & 4 & 8 \\ 1 & 3 & 1 & 6 \end{array} \right] \overrightarrow{R_1 \cdot \frac{-1}{12}} \left[ \begin{array}{rrrr} 0 & 1 & \frac{1}{4} & \frac{1}{2} \\ 0 & 0 & 4 & 8 \\ 1 & 3 & 1 & 6 \end{array} \right] $$

$$ \left[ \begin{array}{rrrr} 0 & 1 & \frac{1}{4} & \frac{1}{2} \\ 0 & 0 & 4 & 8 \\ 1 & 3 & 1 & 6 \end{array} \right] \overrightarrow{R_2 \cdot \frac{1}{4}} \left[ \begin{array}{rrrr} 0 & 1 & \frac{1}{4} & \frac{1}{2} \\ 0 & 0 & 1 & 2 \\ 1 & 3 & 1 & 6 \end{array} \right] \overrightarrow{R_1 \leftrightarrow R_3} \left[ \begin{array}{rrrr} 1 & 3 & 1 & 6 \\ 0 & 0 & 1 & 2 \\ 0 & 1 & \frac{1}{4} & \frac{1}{2} \end{array} \right] $$

$$ \left[ \begin{array}{rrrr} 1 & 3 & 1 & 6 \\ 0 & 0 & 1 & 2 \\ 0 & 1 & \frac{1}{4} & \frac{1}{2} \end{array} \right] \overrightarrow{R_2 \leftrightarrow R_3} \left[ \begin{array}{rrrr} 1 & 3 & 1 & 6 \\ 0 & 1 & \frac{1}{4} & \frac{1}{2} \\ 0 & 0 & 1 & 2 \end{array} \right] $$

$$ (d) \left[ \begin{array}{rrrr} -1 & 6 & -1 & -1 \\ 3 & -18 & 1 & 0 \\ 2 & -12 & 3 & 0 \end{array} \right] $$

$$ \left[ \begin{array}{rrrr} -1 & 6 & -1 & -1 \\ 3 & -18 & 1 & 0 \\ 2 & -12 & 3 & 0 \end{array} \right] \overrightarrow{R_1 \cdot (-1)} \left[ \begin{array}{rrrr} 1 & -6 & 1 & 1 \\ 3 & -18 & 1 & 0 \\ 2 & -12 & 3 & 0 \end{array} \right] \overrightarrow{R_2 - 3R_1} \left[ \begin{array}{rrrr} 1 & -6 & 1 & 1 \\ 0 & 0 & -2 & -3 \\ 2 & -12 & 3 & 0 \end{array} \right] $$

$$ \left[ \begin{array}{rrrr} 1 & -6 & 1 & 1 \\ 0 & 0 & -2 & -3 \\ 2 & -12 & 3 & 0 \end{array} \right] \overrightarrow{R_3 - 2R_1} \left[ \begin{array}{rrrr} 1 & -6 & 1 & 1 \\ 0 & 0 & -2 & -3 \\ 0 & 0 & 1 & -2 \end{array} \right] \overrightarrow{R_2 + 2R_3} \left[ \begin{array}{rrrr} 1 & -6 & 1 & 1 \\ 0 & 0 & 0 & -7 \\ 0 & 0 & 1 & -2 \end{array} \right] $$

$$ \left[ \begin{array}{rrrr} 1 & -6 & 1 & 1 \\ 0 & 0 & 0 & -7 \\ 0 & 0 & 1 & -2 \end{array} \right] \overrightarrow{R_2 \cdot - \frac{1}{7}} \left[ \begin{array}{rrrr} 1 & -6 & 1 & 1 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & -2 \end{array} \right] \overrightarrow{R_2 \leftrightarrow R_3} \left[ \begin{array}{rrrr} 1 & -6 & 1 & 1 \\ 0 & 0 & 1 & -2 \\ 0 & 0 & 0 & 1 \end{array} \right] $$

3. [2 pts each] For each of the following matrices (already in RREF) parameterize all the solutions to the corresponding system of equations. Write your solution in vector form.

$ (a) \left[ \begin{array}{rrrr} 1 & 0 & 3 & | & 8 \\ 0 & 1 & 2 & | & 2 \end{array} \right] $

Parametrize:
$x + 3z = 8$
$y + 2z = 2$

Find leading points
$x = 8 - 3z$
$y = 2 - 2z$
z = s

Vector form:
$ \left[ \begin{array}{r} x \\ y \\ z \end{array} \right] = \left[ \begin{array}{r} 8 \\ 2 \\ 0 \end{array} \right] + s \left[ \begin{array}{r} -3 \\ -2 \\ 1 \end{array} \right] $

$ (b) \left[ \begin{array}{rrrr} 1 & -4 & 0 & - \frac{3}{2} & | & 5 \\ 0 & 0 & 1 & 6 & | & \frac{1}{9} \end{array} \right] $

Parametrize:
$x_1 - 4x_2 - \frac{3}{2} x_4 = 5$
$x_3 + 6x_4 = \frac{1}{9}$

Find Leading points:
$x_1 = 4x_2 + \frac{3}{2} x_4 + 5$
$x_2 = t$
$x_3 = - 6x_4 + \frac{1}{9}$
$x_4 = s$

Vector:
$ \left[ \begin{array}{r} x_1 \\ x_2 \\ x_3 \\ x_4 \end{array} \right] = \left[ \begin{array}{r} 5 \\ 0 \\ \frac{1}{9} \\ 0 \end{array} \right] + t \left[ \begin{array}{r} 4 \\ 1 \\ 0 \\ 0 \end{array} \right] + s \left[ \begin{array}{r} \frac{3}{2} \\ 0 \\ -6 \\ 1 \end{array} \right] $

$ (c) \left[ \begin{array}{rrrr} 1 & 0 & 3 & 0 & 1 & | & -5 \\ 0 & 1 & 2 & 0 & 8 & | & 9 \\ 0 & 0 & 0 & 1 & 7 & | & 4 \end{array} \right] $

Parametrize
$x_1 + 3x_3 + x_5 = - 5$
$x_2 + 2x_3 + 8x_5 = 9$
$x_4 + 7x_5 = 4$

Find Leading Variables:
$x_1 = - 3x_3 - x_5 - 5$
$x_2 = 9 - 2x_3 - 8x_5$
$x_3 = t$
$x_4 = 4 - 7x_5$
$x_5 = s$

Vector Form:
$ \left[ \begin{array}{r} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{array} \right] = \left[ \begin{array}{r} -5 \\ 9 \\ 0 \\ 4 \\ 0 \end{array} \right] + t \left[ \begin{array}{r} -3 \\ -2 \\ 1 \\ 0 \\ 0 \end{array} \right] + s \left[ \begin{array}{r} -1 \\ -8 \\ 0 \\ -7 \\ 1 \end{array} \right] $

$ (d) \left[ \begin{array}{rrrr} 1 & -2 & 0 & 3 & 0 & 11 & | & -7 \\ 0 & 0 & 1 & 4 & 0 & 6 & | & 21 \\ 0 & 0 & 0 & 0 & 1 & -9 & | & 14 \end{array} \right] $

Parametrize:
$x_1 - 2x_2 + 3x_4 + 11x_6 = -7$
$x_3 + 4x_4 + 6x_6 = 21$
$x_5 - 9x_6 = 14$

Find Leading Variables:
$x_1 = 2x_2 - 3x_4 - 11x_6 - 7$
$x_2 = t$
$x_3 = - 4x_4 - 6x_6 + 21$
$x_4 = s$
$x_5 = 9x_6 + 14$
$x_6 = u$

Vector
$ \left[ \begin{array}{r} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \\ x_6 \end{array} \right] = \left[ \begin{array}{r} -7 \\ 0 \\ 21 \\ 0 \\ 14 \\ 0 \end{array} \right] + t \left[ \begin{array}{r} 2 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \end{array} \right] + s \left[ \begin{array}{r} -3 \\ 0 \\ -4 \\ 1 \\ 0 \\ 0 \end{array} \right] + u \left[ \begin{array}{r} -11 \\ 0 \\ -6 \\ 0 \\ 9 \\ 1 \end{array} \right] $

4. [2 pts each] Pigeons are sold at a rate of 5 for 3 coins, swans at a rate of 7 for 5 coins, and peacocks at the rate of 1 for 3 coins. A man was told to bring 100 birds costing 100 coins for the amusement of the King’s son. How many of each kind does he buy? (This is a version of a problem from a 9th century Indian text.)

(a) If x is the number of pigeons, y the number of swans, and z the number of peacocks, write down the corresponding linear equations and the augmented matrix for the problem.

$x + y + z = 100 :=$ number of birds
$\frac{3}{5}x + \frac{5}{7}y + 3z = 100 := $ total costs

$ \left[ \begin{array}{rrrrr} 1 & 1 & 1 & | & 100 \\ \frac{3}{5} & \frac{5}{7} & 3 & | & 100 \end{array} \right] $

(b) Parameterize the solutions to the equations, where $x$, $y$, and $z$ are real numbers.

$ \left[ \begin{array}{rrrrr} 1 & 1 & 1 & | & 100 \\ \frac{3}{5} & \frac{5}{7} & 3 & | & 100 \end{array} \right] \overrightarrow{R_2 \cdot \frac{5}{3}} \left[ \begin{array}{rrrrr} 1 & 1 & 1 & | & 100 \\ 1 & \frac{25}{21} & 5 & | & \frac{500}{3} \end{array} \right] \overrightarrow{R_2 - R_1} \left[ \begin{array}{rrrrr} 1 & 1 & 1 & | & 100 \\ 0 & \frac{4}{21} & 4 & | & \frac{200}{3} \end{array} \right] \overrightarrow{R_2 \cdot \frac{21}{4}} \left[ \begin{array}{rrrrr} 1 & 1 & 1 & | & 100 \\ 0 & 1 & 21 & | & 350 \end{array} \right] $

$x + y + z = 100$
$y + 21z = 350$

$x = 100 - y - z = 100 - (350 - 21z) - z = - 250 + 20z$
$y = 350 - 21z$
$z = s$

$ \left[ \begin{array}{r} x \\ y \\ z \end{array} \right] = \left[ \begin{array}{r} -250 \\ 350 \\ 0 \end{array} \right] + s \left[ \begin{array}{r} 20 \\ -21 \\ 1 \end{array} \right] $

(c) Finally, solve the problem of the riddle. Since $x$, $y$, and $z$ are the numbers of birds, they must be integers, greater than or equal to zero. Also, according to the conditions of the problem, $x$ must be a multiple of 5, and y a multiple of 7. There is more than one solution; find them all.

Through pattern recognition and a bit of trial and error with using the parametric form and the nature of the riddle (like $x$, $y$ and $z$ needing to be positive integers), I found these four solutions - I also believe these are the only valid solutions:

$x = 70$
$y = 14$
$z = 16$

$x = 50$
$y = 35$
$z = 15$

$x = 30$
$y = 56$
$z = 14$

$x = 10$
$y = 77$
$z = 13$

---

1. Let $f(x) = x^2 - 2$. Use the Intermediate Value Theorem to show that there is $x > 0$ so that $f(x) = 0$. What is another name for this $x$?

Another name for x in this context is an x-intercept or root, a point where the function experiences a sign change. To prove there is a root from $x > 0 $, we prove that the function changes sign at some point during this set ($ x > 0$ is the same as $ x \in (0, \infty)$).

$f(0) = (0)^2 - 2 = -2$
we use an arbitrarily high number in place of $\infty$: $f(1000) = (1000)^2 - 2 = 999998$

$\therefore$ since there is a sign changes between f(0) and f(1000), then there must be a root, and therefore a solution.

$ 0 = x^2 - 2 \Rightarrow 0 = (x + \sqrt{2})(x - \sqrt{2}) \Rightarrow x = \sqrt{2} \text{ and } x = - \sqrt{2}$

$ - \sqrt{2} \notin (0, \infty)$. but $ \sqrt{2} \in (0, \infty)$

$\therefore \sqrt{2} > 0$ and $f(\sqrt{2}) = 0$.

2. Use the Intermediate Value Theorem to show that there is a number $x$ such that $1 + \sin x = x$. Use a calculator or a computer to estimate x to two decimal places

We can convert the relation into a function and use the intermediate value theorem to prove there is a root and therefore a solution to it.

$ 1 + \sin x = x \Rightarrow 1 + \sin x - x = 0$

Let $f(x) = 1 + \sin x - x$

Let $x = 0$
$f(0) = 1 + \sin 0 - 0 = 1$

Let $x = 10$ (this was picked arbitrarily)
$f(10) = 1 + \sin 10 - 10 = ~ -8.83$

$\therefore$ since the sign changes between f(0) and f(10), then there must be a root, and therefore a solution.

Using a graphing calculator, I found x = ~ 1.93

3. Let us recall the definition of a limit at $ -\infty$. We say $ \lim\limits_{x \to - \infty} f(x) = L$ if for every $\epsilon > 0$ there is $M > 0$ such that $| f(x) - L | < \epsilon$ whenever $ x < -M$. Let $f(x) = -x^{-3}$. Using the definition above, find the limit: $ \lim\limits_{x \to - \infty} f(x).$ What dose this say about the graph of f?

Conjecture: $ \lim\limits_{x \to - \infty} -x^{-3} = 0$

$ | f(x) - L | < \epsilon$
$ \Leftrightarrow | -x^{-3} - 0 | < \epsilon$
$ \Leftrightarrow | -x^{-3} | < \epsilon$
$ \Leftrightarrow -x^{-3} < \epsilon$ (because x is assumed to be negative)
$ \Leftrightarrow -\frac{1}{x^3} < \epsilon$
$ \Leftrightarrow -1 > \epsilon x^3$
$ \Leftrightarrow -\frac{1}{\epsilon} > x^3$
$ \Leftrightarrow \sqrt[3]{-\frac{1}{\epsilon}} > x$
$ \Leftrightarrow -\sqrt[3]{\frac{1}{\epsilon}} > x$

Let $\sqrt[3]{\frac{1}{\epsilon}} \Rightarrow - M > x$

$\therefore \lim\limits_{x \to - \infty} -x^{-3} = 0$

4. Recall our definition: $\lim\limits_{ x \to a} f(x) = \infty$, if for every $ M > 0$, there is $ \delta > 0$ such that $f(x) > M$ whenever $ 0 < | x - a | < \delta$. Let $ f(x) = - ln(|x|)$ for $ x \neq 0$. Using the definition show that $ \lim\limits_{x \to 0} f(x) = \infty$.

$f(x) < M$
$ \Leftrightarrow -ln(|x|) < -M$
$ \Leftrightarrow ln(|x|) < -M$
$ \Leftrightarrow |x| < e^{-M}$

$\therefore \delta = e^{-M}$

$ | x - a | < \delta$
$ \Leftrightarrow | x - 0 | < \delta$
$ \Leftrightarrow |x| < \delta$

$\therefore \lim\limits_{x \to 0} f(x) = \infty$ according to the definition of a limit that equals infinity.

---

1. [2 pts each] Find the ranks of the following matrices.

(a) $ \left[ \begin{array}{rrrr} 2 & 1 & 2 & 5 \\ 1 & 0 & 4 & 1 \\ 2 & 1 & 3 & 5 \end{array} \right] \overrightarrow{R_3 - R_1} \left[ \begin{array}{rrrr} 2 & 1 & 2 & 5 \\ 1 & 0 & 4 & 1 \\ 0 & 0 & 1 & 0 \end{array} \right] \overrightarrow{R_1 - 2R_2} \left[ \begin{array}{rrrr} 0 & 1 & -6 & 3 \\ 1 & 0 & 4 & 1 \\ 0 & 0 & 1 & 0 \end{array} \right] \overrightarrow{R_1 + 6R_3, R_2 - 4R_3} \left[ \begin{array}{rrrr} 0 & 1 & 0 & 3 \\ 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{array} \right] \overrightarrow{R_1 \leftrightarrow R_2} \left[ \begin{array}{rrrr} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 0 \end{array} \right] $

$\therefore$ the matrix has 3 independent variables $\Rightarrow$ rank(a) = 3

(b) $ \left[ \begin{array}{rrrr} 2 & 1 & 2 \\ 1 & 0 & 1 \\ 2 & 4 & 3 \\ 5 & 1 & 5 \end{array} \right] \overrightarrow{R_1 \leftrightarrow R_2} \left[ \begin{array}{rrrr} 1 & 0 & 1 \\ 2 & 1 & 2 \\ 2 & 4 & 3 \\ 5 & 1 & 5 \end{array} \right] \overrightarrow{R_2 - R_3} \left[ \begin{array}{rrrr} 1 & 0 & 1 \\ 0 & -3 & -1 \\ 2 & 4 & 3 \\ 5 & 1 & 5 \end{array} \right] \overrightarrow{R_3 - 2R_1} \left[ \begin{array}{rrrr} 1 & 0 & 1 \\ 0 & -3 & -1 \\ 0 & 4 & 1 \\ 5 & 1 & 5 \end{array} \right] \overrightarrow{R_4 - 5R_1} \left[ \begin{array}{rrrr} 1 & 0 & 1 \\ 0 & -3 & -1 \\ 0 & 4 & 1 \\ 0 & 1 & 0 \end{array} \right] \overrightarrow{R_2 + 3R_4} \left[ \begin{array}{rrrr} 1 & 0 & 1 \\ 0 & 0 & -1 \\ 0 & 4 & 1 \\ 0 & 1 & 0 \end{array} \right] \overrightarrow{R_3 - 4R_4} \left[ \begin{array}{rrrr} 1 & 0 & 1 \\ 0 & 0 & -1 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{array} \right] \overrightarrow{R_2 + R_3, R_1 - R_3} \left[ \begin{array}{rrrr} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{array} \right] $

$ \left[ \begin{array}{rrrr} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{array} \right] \overrightarrow{R_2 \leftrightarrow R_4} \left[ \begin{array}{rrrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{array} \right] $

$\therefore$ the matrix has 3 independent variables $\Rightarrow$ rank(b) = 3

(c) $ \left[ \begin{array}{rrrrr} 1 & 0 & 1 & -1 & 6 \\ 2 & -1 & 5 & -1 & 7 \\ -1 & 1 & -4 & 1 & -3 \\ 0 & 1 & -3 & 1 & 1 \end{array} \right] \overrightarrow{R_2 - 2R_1} \left[ \begin{array}{rrrrr} 1 & 0 & 1 & -1 & 6 \\ 0 & -1 & 3 & 1 & -5 \\ -1 & 1 & -4 & 1 & -3 \\ 0 & 1 & -3 & 1 & 1 \end{array} \right] \overrightarrow{R_3 + R_1} \left[ \begin{array}{rrrrr} 1 & 0 & 1 & -1 & 6 \\ 0 & -1 & 3 & 1 & -5 \\ 0 & 1 & -3 & 0 & 3 \\ 0 & 1 & -3 & 1 & 1 \end{array} \right] \overrightarrow{R_3 + R_2} \left[ \begin{array}{rrrrr} 1 & 0 & 1 & -1 & 6 \\ 0 & -1 & 3 & 1 & -5 \\ 0 & 0 & 0 & 1 & -2 \\ 0 & 1 & -3 & 1 & 1 \end{array} \right] $

$ \left[ \begin{array}{rrrrr} 1 & 0 & 1 & -1 & 6 \\ 0 & -1 & 3 & 1 & -5 \\ 0 & 0 & 0 & 1 & -2 \\ 0 & 1 & -3 & 1 & 1 \end{array} \right] \overrightarrow{R_4 + R_2} \left[ \begin{array}{rrrrr} 1 & 0 & 1 & -1 & 6 \\ 0 & -1 & 3 & 1 & -5 \\ 0 & 0 & 0 & 1 & -2 \\ 0 & 0 & 0 & 2 & -4 \end{array} \right] \overrightarrow{R_4 - 2R_3} \left[ \begin{array}{rrrrr} 1 & 0 & 1 & -1 & 6 \\ 0 & -1 & 3 & 1 & -5 \\ 0 & 0 & 0 & 1 & -2 \\ 0 & 0 & 0 & 0 & 0 \end{array} \right] \overrightarrow{R_2 \cdot -1} \left[ \begin{array}{rrrrr} 1 & 0 & 1 & -1 & 6 \\ 0 & 1 & -3 & -1 & 5 \\ 0 & 0 & 0 & 1 & -2 \\ 0 & 0 & 0 & 0 & 0 \end{array} \right] \overrightarrow{R_1 + R_3, R_2 + R_3} \left[ \begin{array}{rrrrr} 1 & 0 & 1 & 0 & 4 \\ 0 & 1 & -3 & 0 & 3 \\ 0 & 0 & 0 & 1 & -2 \\ 0 & 0 & 0 & 0 & 0 \end{array} \right] $

$\therefore$ the matrix has 3 independent variables $\Rightarrow$ rank(c) = 3

(d) Suppose the matrices in (a), (b), and (c) above are the coefficient matrices of a system of linear equations. Assuming that each of the systems has solutions, how many free parameters must the general solution to each of the systems have?

The amount of free parameters would be the the amount of columns that doesn’t have an independent variable.

a) 1
b) 0
c) 2

2. [2 pts each] Find the rank of the following matrices, where k is a real number (The answer depends on the values of k.)

(a) $ \left[ \begin{array}{rrrrr} k & 1 & 2 \\ 1 & 1 & 1 \\ -1 & 1 & (1 - k) \end{array} \right] $

$ \left[ \begin{array}{rrrrr} k & 1 & 2 \\ 1 & 1 & 1 \\ -1 & 1 & (1 - k) \end{array} \right] \overrightarrow{R_1 \cdot \frac{1}{k}} \left[ \begin{array}{rrrrr} 1 & \frac{1}{k} & \frac{2}{k} \\ 1 & 1 & 1 \\ -1 & 1 & (1 - k) \end{array} \right] \overrightarrow{R_2 - R_1} \left[ \begin{array}{rrrrr} 1 & \frac{1}{k} & \frac{2}{k} \\ 0 & \frac{k - 1}{k} & \frac{k -2}{k} \\ -1 & 1 & (1 - k) \end{array} \right] \overrightarrow{R_3 + R_1} \left[ \begin{array}{rrrrr} 1 & \frac{1}{k} & \frac{2}{k} \\ 0 & \frac{k - 1}{k} & \frac{k -2}{k} \\ 0 & \frac{1 + k}{k} & 1 - k + \frac{2}{k} \end{array} \right] \overrightarrow{R_2 \cdot \frac{k}{k - 1}} \left[ \begin{array}{rrrrr} 1 & \frac{1}{k} & \frac{2}{k} \\ 0 & 1 & \frac{k - 2}{k - 1} \\ 0 & \frac{1 + k}{k} & 1 - k + \frac{2}{k} \end{array} \right] \overrightarrow{R_1 - \frac{1}{k}R_2} \left[ \begin{array}{rrrrr} 1 & 0 & \frac{1}{k - 1} \\ 0 & 1 & \frac{k - 2}{k - 1} \\ 0 & \frac{1 + k}{k} & 1 - k + \frac{2}{k} \end{array} \right] $

$ \left[ \begin{array}{rrrrr} 1 & 0 & \frac{1}{k - 1} \\ 0 & 1 & \frac{k - 2}{k - 1} \\ 0 & \frac{1 + k}{k} & 1 - k + \frac{2}{k} \end{array} \right] \overrightarrow{R_3 - \frac{1 + k}{k}R_2} \left[ \begin{array}{rrrrr} 1 & 0 & \frac{1}{k - 1} \\ 0 & 1 & \frac{k - 2}{k - 1} \\ 0 & 0 & \frac{k - k^2 + 2}{k - 1} \end{array} \right] \overrightarrow{R_3 \cdot \frac{k - 1}{k - k^2 + 2}} \left[ \begin{array}{rrrrr} 1 & 0 & \frac{1}{k - 1} \\ 0 & 1 & \frac{k - 2}{k - 1} \\ 0 & 0 & 1 \end{array} \right] \overrightarrow{R_2 - \frac{k - 1}{k - 2}R_3} \left[ \begin{array}{rrrrr} 1 & 0 & \frac{1}{k - 1} \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right] \overrightarrow{R_1 - (k - 1)R_3} \left[ \begin{array}{rrrrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right] $

$\therefore$ the matrix has a rank of 3 when $k \neq -1, 0, 1, 2$

But what if $k = -1, 0, 1, 2$

if $k = -1$
$ \left[ \begin{array}{rrrrr} k & 1 & 2 \\ 1 & 1 & 1 \\ -1 & 1 & (1 - k) \end{array} \right] = \left[ \begin{array}{rrrrr} -1 & 1 & 2 \\ 1 & 1 & 1 \\ -1 & 1 & 2 \end{array} \right] \overrightarrow{R_1 \cdot - 1} \left[ \begin{array}{rrrrr} 1 & -1 & -2 \\ 1 & 1 & 1 \\ -1 & 1 & 2 \end{array} \right] \overrightarrow{R_2 - R_1} \left[ \begin{array}{rrrrr} 1 & -1 & -2 \\ 0 & 2 & 3 \\ -1 & 1 & 2 \end{array} \right] \overrightarrow{R_2 + R_1} \left[ \begin{array}{rrrrr} 1 & -1 & -2 \\ 0 & 2 & 3 \\ 0 & 0 & 0 \end{array} \right] \overrightarrow{R_2 \cdot \frac{1}{2}} \left[ \begin{array}{rrrrr} 1 & -1 & -2 \\ 0 & 1 & \frac{3}{2} \\ 0 & 0 & 0 \end{array} \right] \overrightarrow{R_1 + R_2} \left[ \begin{array}{rrrrr} 1 & 0 & \frac{1}{2} \\ 0 & 1 & \frac{3}{2} \\ 0 & 0 & 0 \end{array} \right] $

$\therefore$ when $k = -1$, the rank of the matrix is 2

if $k = 0$
$ \left[ \begin{array}{rrrrr} k & 1 & 2 \\ 1 & 1 & 1 \\ -1 & 1 & (1 - k) \end{array} \right] = \left[ \begin{array}{rrrrr} 0 & 1 & 2 \\ 1 & 1 & 1 \\ -1 & 1 & 1 \end{array} \right] \overrightarrow{R_3 + R_2} \left[ \begin{array}{rrrrr} 0 & 1 & 2 \\ 1 & 1 & 1 \\ 0 & 2 & 2 \end{array} \right] \overrightarrow{R_1 \leftrightarrow R_2} \left[ \begin{array}{rrrrr} 1 & 1 & 1 \\ 0 & 1 & 2 \\ 0 & 2 & 2 \end{array} \right] \overrightarrow{R_1 - R_2} \left[ \begin{array}{rrrrr} 1 & 0 & -1 \\ 0 & 1 & 2 \\ 0 & 2 & 2 \end{array} \right] \overrightarrow{R_3 - 2R_2} \left[ \begin{array}{rrrrr} 1 & 0 & -1 \\ 0 & 1 & 2 \\ 0 & 0 & -2 \end{array} \right] \overrightarrow{R_2 + R_3} \left[ \begin{array}{rrrrr} 1 & 0 & -1 \\ 0 & 1 & 0 \\ 0 & 0 & -2 \end{array} \right] \overrightarrow{R_3 \cdot - \frac{1}{2}} \left[ \begin{array}{rrrrr} 1 & 0 & -1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right] \overrightarrow{R_1 + R_3} \left[ \begin{array}{rrrrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right] $

$\therefore$ when $k = 0$, the rank of the matrix is 3

if $k = 1$, $ \left[ \begin{array}{rrrrr} k & 1 & 2 \\ 1 & 1 & 1 \\ -1 & 1 & (1 - k) \end{array} \right] = \left[ \begin{array}{rrrrr} 1 & 1 & 2 \\ 1 & 1 & 1 \\ -1 & 1 & 0 \end{array} \right] \overrightarrow{R_2 - R_1} \left[ \begin{array}{rrrrr} 1 & 1 & 2 \\ 0 & 0 & -1 \\ -1 & 1 & 0 \end{array} \right] \overrightarrow{R_3 + R_1} \left[ \begin{array}{rrrrr} 1 & 1 & 2 \\ 0 & 0 & -1 \\ 0 & 2 & 2 \end{array} \right] \overrightarrow{R_2 \leftrightarrow R_3} \left[ \begin{array}{rrrrr} 1 & 1 & 2 \\ 0 & 2 & 2 \\ 0 & 0 & -1 \end{array} \right] \overrightarrow{R_2 \cdot \frac{1}{2}} \left[ \begin{array}{rrrrr} 1 & 1 & 2 \\ 0 & 1 & 1 \\ 0 & 0 & -1 \end{array} \right] \overrightarrow{R_2 - R_1} \left[ \begin{array}{rrrrr} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & -1 \end{array} \right] \overrightarrow{R_3 \cdot -1} \left[ \begin{array}{rrrrr} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{array} \right] \overrightarrow{R_1 - R_3} \left[ \begin{array}{rrrrr} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{array} \right] $

$ \left[ \begin{array}{rrrrr} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{array} \right] \overrightarrow{R_2 - R_3} \left[ \begin{array}{rrrrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right] $

$\therefore$ when $k = 1$, the rank of the matrix is 3

if $k = 2$, $ \left[ \begin{array}{rrrrr} k & 1 & 2 \\ 1 & 1 & 1 \\ -1 & 1 & (1 - k) \end{array} \right] = \left[ \begin{array}{rrrrr} 2 & 1 & 2 \\ 1 & 1 & 1 \\ -1 & 1 & -1 \end{array} \right] \overrightarrow{R_1 \cdot \frac{1}{2}} \left[ \begin{array}{rrrrr} 1 & \frac{1}{2} & 1 \\ 1 & 1 & 1 \\ -1 & 1 & -1 \end{array} \right] \overrightarrow{R_2 - R_1} \left[ \begin{array}{rrrrr} 1 & \frac{1}{2} & 1 \\ 0 & \frac{1}{2} & 0 \\ -1 & 1 & -1 \end{array} \right] \overrightarrow{R_3 + R_1} \left[ \begin{array}{rrrrr} 1 & \frac{1}{2} & 1 \\ 0 & \frac{1}{2} & 0 \\ 0 & \frac{3}{2} & 0 \end{array} \right] \overrightarrow{R_2 \cdot 2} \left[ \begin{array}{rrrrr} 1 & \frac{1}{2} & 1 \\ 0 & 1 & 0 \\ 0 & \frac{3}{2} & 0 \end{array} \right] \overrightarrow{R_1 - \frac{1}{2}R_2} \left[ \begin{array}{rrrrr} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & \frac{3}{2} & 0 \end{array} \right] \overrightarrow{R_3 - \frac{3}{2}R_2} \left[ \begin{array}{rrrrr} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array} \right] $

$\therefore$ when $k = 2$, the rank of the matrix is 2

$\therefore$ when $k \neq 2 \text{ or } -1$, then the rank of the matrix is 3. When $k = -1$, or $k = 2$, the rank of the matrix is 2.

(b) $ \left[ \begin{array}{rrrrr} 1 & 1 & k & 1 \\ 1 & k & 1 & 1 \\ k & 1 & 1 & -2 \end{array} \right] $

$ \left[ \begin{array}{rrrrr} 1 & 1 & k & 1 \\ 1 & k & 1 & 1 \\ k & 1 & 1 & -2 \end{array} \right] \overrightarrow{R_2 - R_1} \left[ \begin{array}{rrrrr} 1 & 1 & k & 1 \\ 0 & k - 1 & 1 - k & 0 \\ k & 1 & 1 & -2 \end{array} \right] \overrightarrow{R_3 - kR_1} \left[ \begin{array}{rrrrr} 1 & 1 & k & 1 \\ 0 & k - 1 & 1 - k & 0 \\ 0 & 1 - k & 1 - k^2 & -2 - k \end{array} \right] \overrightarrow{R_2 \cdot \frac{1}{k - 1}} \left[ \begin{array}{rrrrr} 1 & 1 & k & 1 \\ 0 & 1 & -1 & 0 \\ 0 & 1 - k & 1 - k^2 & -2 - k \end{array} \right] \overrightarrow{R_1 - R_2} \left[ \begin{array}{rrrrr} 1 & 0 & k + 1 & 1 \\ 0 & 1 & -1 & 0 \\ 0 & 1 - k & 1 - k^2 & -2 - k \end{array} \right] $

$ \left[ \begin{array}{rrrrr} 1 & 0 & k + 1 & 1 \\ 0 & 1 & -1 & 0 \\ 0 & 1 - k & 1 - k^2 & -2 - k \end{array} \right] \overrightarrow{R_3 - (1 - k)R_2} \left[ \begin{array}{rrrrr} 1 & 0 & k + 1 & 1 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 2 - k^2 - k & -2 - k \end{array} \right] \overrightarrow{R_3 \cdot \frac{1}{2 - k^2 - k}} \left[ \begin{array}{rrrrr} 1 & 0 & k + 1 & 1 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 1 & \frac{1}{ k - 1} \end{array} \right] \overrightarrow{R_1 - (k + 1)R_3} \left[ \begin{array}{rrrrr} 1 & 0 & 0 & 1 - \frac{k + 1}{k - 2} \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 1 & \frac{1}{ k - 1} \end{array} \right] \overrightarrow{R_2 + R_3} \left[ \begin{array}{rrrrr} 1 & 0 & 0 & 1 - \frac{k + 1}{k - 2} \\ 0 & 1 & 0 & \frac({1}{k - 1}) \\ 0 & 0 & 1 & \frac{1}{ k - 1} \end{array} \right] $

$\therefore$ when $k \neq 1$ or -2, then the rank of the matrix is 3

if $k = 1$,
$ \left[ \begin{array}{rrrrr} 1 & 1 & k & 1 \\ 1 & k & 1 & 1 \\ k & 1 & 1 & -2 \end{array} \right] = \left[ \begin{array}{rrrrr} 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & -2 \end{array} \right] \overrightarrow{R_2 - R_1} \left[ \begin{array}{rrrrr} 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & -2 \end{array} \right] \overrightarrow{R_3 - R_1} \left[ \begin{array}{rrrrr} 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & -3 \end{array} \right] \overrightarrow{R_3 \cdot - \frac{1}{3}} \left[ \begin{array}{rrrrr} 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right] \overrightarrow{R_1 - R_3} \left[ \begin{array}{rrrrr} 1 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right] $

$\therefore$ when $k = 1$, then the rank of the matrix is 2

if $k = -2$,
$ \left[ \begin{array}{rrrrr} 1 & 1 & k & 1 \\ 1 & k & 1 & 1 \\ k & 1 & 1 & -2 \end{array} \right] = \left[ \begin{array}{rrrrr} 1 & 1 & -2 & 1 \\ 1 & -2 & 1 & 1 \\ -2 & 1 & 1 & -2 \end{array} \right] \overrightarrow{R_2 - R_1} \left[ \begin{array}{rrrrr} 1 & 1 & -2 & 1 \\ 0 & -3 & 3 & 0 \\ -2 & 1 & 1 & -2 \end{array} \right] \overrightarrow{R_3 + 2R_1} \left[ \begin{array}{rrrrr} 1 & 1 & -2 & 1 \\ 0 & -3 & 3 & 0 \\ 0 & 3 & -3 & 0 \end{array} \right] \overrightarrow{R_2 \cdot - \frac{1}{3}} \left[ \begin{array}{rrrrr} 1 & 1 & -2 & 1 \\ 0 & 1 & -1 & 0 \\ 0 & 3 & -3 & 0 \end{array} \right] \overrightarrow{R_1 - R_2} \left[ \begin{array}{rrrrr} 1 & 0 & -1 & 1 \\ 0 & 1 & -1 & 0 \\ 0 & 3 & -3 & 0 \end{array} \right] \overrightarrow{R_3 - 3R_2} \left[ \begin{array}{rrrrr} 1 & 0 & -1 & 1 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right] $

$\therefore$ when $k = -2$, then the rank of the matrix is 2

$\therefore$ when $k \neq -2 \text{ or } 1$, then the rank of the matrix is 3. When $k = -2$, or $k = 1$, the rank of the matrix is 2.

3. [2 pts each] In each of the following three cases, determine of the vector w is a linear combination of the others and if it is, write the vector w as a linear combination of the others.

(a) $w = (3, 6, 11)$, $v_1 = (1, 2, 4)$, $v_2 = (−1, 1, 0)$, $v_3 = (0, 1, 1)$

Express as an equation:
$ w = av_1 + bv_2 + cv_3$

$ \left( \begin{array}{r} 3 \\ 6 \\ 11 \end{array} \right) = a \left( \begin{array}{r} 1 \\ 2 \\ 4 \end{array} \right) + b \left( \begin{array}{r} -1 \\ 1 \\ 0 \end{array} \right) + c \left( \begin{array}{r} 0 \\ 1 \\ 1 \end{array} \right) $

Write equations as augmented matrix:
$ \left[ \begin{array}{rrrrr} 1 & -1 & 0 & | & 3 \\ 2 & 1 & 1 & | & 6 \\ 4 & 0 & 1 & | & 11 \end{array} \right] $

Convert matrix to RREF:
$ \left[ \begin{array}{rrrrr} 1 & -1 & 0 & | & 3 \\ 2 & 1 & 1 & | & 6 \\ 4 & 0 & 1 & | & 11 \end{array} \right] \overrightarrow{R_2 - 2R_1} \left[ \begin{array}{rrrrr} 1 & -1 & 0 & | & 3 \\ 0 & 3 & 1 & | & 0 \\ 4 & 0 & 1 & | & 11 \end{array} \right] \overrightarrow{R_4 - 2R_1} \left[ \begin{array}{rrrrr} 1 & -1 & 0 & | & 3 \\ 0 & 3 & 1 & | & 0 \\ 0 & 4 & 1 & | & -1 \end{array} \right] \overrightarrow{R_2 \cdot \frac{1}{3}} \left[ \begin{array}{rrrrr} 1 & -1 & 0 & | & 3 \\ 0 & 1 & \frac{1}{3} & | & 0 \\ 0 & 4 & 1 & | & -1 \end{array} \right] \overrightarrow{R_1 + R_2} \left[ \begin{array}{rrrrr} 1 & 0 & \frac{1}{3} & | & 3 \\ 0 & 1 & \frac{1}{3} & | & 0 \\ 0 & 4 & 1 & | & -1 \end{array} \right] \overrightarrow{R_3 - 4R_2} \left[ \begin{array}{rrrrr} 1 & 0 & \frac{1}{3} & | & 3 \\ 0 & 1 & \frac{1}{3} & | & 0 \\ 0 & 0 & -\frac{1}{3} & | & -1 \end{array} \right] $

$ \left[ \begin{array}{rrrrr} 1 & 0 & \frac{1}{3} & | & 3 \\ 0 & 1 & \frac{1}{3} & | & 0 \\ 0 & 0 & -\frac{1}{3} & | & -1 \end{array} \right] \overrightarrow{R_3 \cdot -3R_2} \left[ \begin{array}{rrrrr} 1 & 0 & \frac{1}{3} & | & 3 \\ 0 & 1 & \frac{1}{3} & | & 0 \\ 0 & 0 & 1 & | & 3 \end{array} \right] \overrightarrow{R_2 -\frac{1}{3}R_2} \left[ \begin{array}{rrrrr} 1 & 0 & \frac{1}{3} & | & 3 \\ 0 & 1 & 0 & | & -1 \\ 0 & 0 & 1 & | & 3 \end{array} \right] \overrightarrow{R_1 -\frac{1}{3}R_2} \left[ \begin{array}{rrrrr} 1 & 0 & 0 & | & 2 \\ 0 & 1 & 0 & | & -1 \\ 0 & 0 & 1 & | & 3 \end{array} \right] $

$a = 2$
$b = -1$
$c = 3$

$\therefore w = 2v_1 - v_2 + 3v_3$

(b) $w = (3, −2, −4, 1)$; $v_1 = (1, 2, 3, 4)$, $v_2 = (1, −1, 1, 1)$, and $v_3 = (2, 0, −3, 1)$

Express as an equation:
$ w = av_1 + bv_2 + cv_3$

$ \left( \begin{array}{r} 3 \\ -2 \\ -4 \\ 1 \end{array} \right) = a \left( \begin{array}{r} 1 \\ 2 \\ 3 \\ 4 \end{array} \right) + b \left( \begin{array}{r} 1 \\ -1 \\ 1 \\ 1 \end{array} \right) + c \left( \begin{array}{r} 2 \\ 0 \\ -3 \\ 1 \end{array} \right) $

Write equations as augmented matrix:
$ \left[ \begin{array}{rrrrr} 1 & 1 & 2 & | & 3 \\ 2 & -1 & 0 & | & -2 \\ 3 & 1 & -3 & | & -4 \\ 4 & 1 & 1 & | & 1 \end{array} \right] $

Convert matrix to RREF:
$ \left[ \begin{array}{rrrrr} 1 & 1 & 2 & | & 3 \\ 2 & -1 & 0 & | & -2 \\ 3 & 1 & -3 & | & -4 \\ 4 & 1 & 1 & | & 1 \end{array} \right] \overrightarrow{R_2 - 2R_1} \left[ \begin{array}{rrrrr} 1 & 1 & 2 & | & 3 \\ 0 & -3 & -4 & | & -8 \\ 3 & 1 & -3 & | & -4 \\ 4 & 1 & 1 & | & 1 \end{array} \right] \overrightarrow{R_3 - 3R_1} \left[ \begin{array}{rrrrr} 1 & 1 & 2 & | & 3 \\ 0 & -3 & -4 & | & -8 \\ 0 & -2 & -9 & | & -13 \\ 4 & 1 & 1 & | & 1 \end{array} \right] \overrightarrow{R_4 - 4R_1} \left[ \begin{array}{rrrrr} 1 & 1 & 2 & | & 3 \\ 0 & -3 & -4 & | & -8 \\ 0 & -2 & -9 & | & -13 \\ 0 & -3 & -7 & | & -11 \end{array} \right] \overrightarrow{R_2 \cdot -\frac{1}{3}} \left[ \begin{array}{rrrrr} 1 & 1 & 2 & | & 3 \\ 0 & 1 & \frac{4}{3} & | & \frac{8}{3} \\ 0 & -2 & -9 & | & -13 \\ 0 & -3 & -7 & | & -11 \end{array} \right] \overrightarrow{R_1 - R_2} \left[ \begin{array}{rrrrr} 1 & 0 & \frac{2}{3} & | & \frac{1}{3} \\ 0 & 1 & \frac{4}{3} & | & \frac{8}{3} \\ 0 & -2 & -9 & | & -13 \\ 0 & -3 & -7 & | & -11 \end{array} \right] $

$ \left[ \begin{array}{rrrrr} 1 & 0 & \frac{2}{3} & | & \frac{1}{3} \\ 0 & 1 & \frac{4}{3} & | & \frac{8}{3} \\ 0 & -2 & -9 & | & -13 \\ 0 & -3 & -7 & | & -11 \end{array} \right] \overrightarrow{R_3 + 2R_2} \left[ \begin{array}{rrrrr} 1 & 0 & \frac{2}{3} & | & \frac{1}{3} \\ 0 & 1 & \frac{4}{3} & | & \frac{8}{3} \\ 0 & 0 & -\frac{19}{3} & | & -\frac{23}{3} \\ 0 & -3 & -7 & | & -11 \end{array} \right] \overrightarrow{R_4 + 3R_2} \left[ \begin{array}{rrrrr} 1 & 0 & \frac{2}{3} & | & \frac{1}{3} \\ 0 & 1 & \frac{4}{3} & | & \frac{8}{3} \\ 0 & 0 & -\frac{19}{3} & | & -\frac{23}{3} \\ 0 & 0 & -3 & | & -3 \end{array} \right] \overrightarrow{R_3 \cdot - \frac{3}{19}} \left[ \begin{array}{rrrrr} 1 & 0 & \frac{2}{3} & | & \frac{1}{3} \\ 0 & 1 & \frac{4}{3} & | & \frac{8}{3} \\ 0 & 0 & 1 & | & \frac{23}{19} \\ 0 & 0 & -3 & | & -3 \end{array} \right] \overrightarrow{R_2 - \frac{4}{3}R_3} \left[ \begin{array}{rrrrr} 1 & 0 & \frac{2}{3} & | & \frac{1}{3} \\ 0 & 1 & 0 & | & \frac{20}{19} \\ 0 & 0 & 1 & | & \frac{23}{19} \\ 0 & 0 & -3 & | & -3 \end{array} \right] \overrightarrow{R_1 - \frac{2}{3}R_3} \left[ \begin{array}{rrrrr} 1 & 0 & 0 & | & - \frac{20}{19} \\ 0 & 1 & 0 & | & \frac{1}{19} \\ 0 & 0 & 1 & | & \frac{23}{19} \\ 0 & 0 & -3 & | & -3 \end{array} \right] $

$ \left[ \begin{array}{rrrrr} 1 & 0 & 0 & | & - \frac{20}{19} \\ 0 & 1 & 0 & | & \frac{1}{19} \\ 0 & 0 & 1 & | & \frac{23}{19} \\ 0 & 0 & -3 & | & -3 \end{array} \right] \overrightarrow{R_4 + 3R_3} \left[ \begin{array}{rrrrr} 1 & 0 & 0 & | & - \frac{9}{19} \\ 0 & 1 & 0 & | & \frac{20}{19} \\ 0 & 0 & 1 & | & \frac{23}{19} \\ 0 & 0 & 0 & | & \frac{12}{19} \end{array} \right] $

$a = - \frac{9}{19}$
$b = \frac{20}{19}$
$c = \frac{23}{19}$
$0 = \frac{12}{19}$?

$\therefore$ w can not be expressed linear combination of $v_1, v_2$ and $v_3$

4. [2 pts each] (a) The span of $v_1 = (1, −1, 0, 0)$, $v_2 = (1, 1, 1, 0)$, and $v_3 = (0, 1, 1, 1)$ is a hyperplane in $\mathbb{R}^4$, i.e., the solutions $(x, y, z, w) \in \mathbb{R}^4$ to an equation $ax + by + cz + dw = 0$. Find the coefficients (a, b, c, d) of this equation.

In theory, there will be at lest one row with no coefficients. so if we can get that row to equal some combination of x, y, z and w, that would give us sufficient coefficient values to make a hyperplane.

$ \left( \begin{array}{r} x \\ y \\ z \\ w \end{array} \right) = a \left( \begin{array}{r} 1 \\ -1 \\ 0 \\ 0 \end{array} \right) + b \left( \begin{array}{r} 1 \\ 1 \\ 1 \\ 0 \end{array} \right) + c \left( \begin{array}{r} 0 \\ 1 \\ 1 \\ 1 \end{array} \right) $

$ \left[ \begin{array}{rrrrr} 1 & 1 & 0 & | & x \\ -1 & 1 & 1 & | & y \\ 0 & 1 & 1 & | & z \\ 0 & 0 & 1 & | & w \end{array} \right] $

$ \left[ \begin{array}{rrrrr} 1 & 1 & 0 & | & x \\ -1 & 1 & 1 & | & y \\ 0 & 1 & 1 & | & z \\ 0 & 0 & 1 & | & w \end{array} \right] \overrightarrow{R_2 + R_1} \left[ \begin{array}{rrrrr} 1 & 1 & 0 & | & x \\ 0 & 2 & 1 & | & y + x \\ 0 & 1 & 1 & | & z \\ 0 & 0 & 1 & | & w \end{array} \right] \overrightarrow{R_2 - R_3} \left[ \begin{array}{rrrrr} 1 & 1 & 0 & | & x \\ 0 & 1 & 0 & | & y + x - z \\ 0 & 1 & 1 & | & z \\ 0 & 0 & 1 & | & w \end{array} \right] \overrightarrow{R_1 - R_2} \left[ \begin{array}{rrrrr} 1 & 0 & 0 & | & z - y \\ 0 & 1 & 0 & | & y + x - z \\ 0 & 1 & 1 & | & z \\ 0 & 0 & 1 & | & w \end{array} \right] \overrightarrow{R_3 - R_2} \left[ \begin{array}{rrrrr} 1 & 0 & 0 & | & z - y \\ 0 & 1 & 0 & | & y + x - z \\ 0 & 0 & 1 & | & 2z - x - y \\ 0 & 0 & 1 & | & w \end{array} \right] $

$ \left[ \begin{array}{rrrrr} 1 & 0 & 0 & | & z - y \\ 0 & 1 & 0 & | & y + x - z \\ 0 & 0 & 1 & | & 2z - x - y \\ 0 & 0 & 1 & | & w \end{array} \right] \overrightarrow{R_4 - R_3} \left[ \begin{array}{rrrrr} 1 & 0 & 0 & | & z - y \\ 0 & 1 & 0 & | & y + x - z \\ 0 & 0 & 1 & | & 2z - x - y \\ 0 & 0 & 0 & | & w - 2z + x + y \end{array} \right] $

a = z - y
b = y + x - z
c = 2z - x - y
0 = w - 2z + x + y = x + y -2z + w

$ \therefore (a, b, c, d) = (1, 1, -2, 1)$

(b) Let $v_1 = (2, −1, 1)$, $v_2 = (0, 1, 4)$, $v_3 = (−2, 2, 3)$. What is $Span(v_1, v_2, v_3)$? Could it be all of $\mathbb{R}^3$?

we can determine if the planes cover all of $\mathbb{R}^3$ by solving for the rank of the points when positioned into a matrix.

$ \left[ \begin{array}{rrr} 2 & 0 & -2 \\ -1 & 1 & 2 \\ 1 & 4 & 3 \end{array} \right] $

$ \left[ \begin{array}{rrr} 2 & 0 & -2 \\ -1 & 1 & 2 \\ 1 & 4 & 3 \end{array} \right] \overrightarrow{R_1 \cdot \frac{1}{2}} \left[ \begin{array}{rrr} 1 & 0 & -1 \\ -1 & 1 & 2 \\ 1 & 4 & 3 \end{array} \right] \overrightarrow{R_2 + R_1} \left[ \begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 1 \\ 1 & 4 & 3 \end{array} \right] \overrightarrow{R_3 - R_1} \left[ \begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 1 \\ 0 & 4 & 4 \end{array} \right] \overrightarrow{R_3 - 4R_2} \left[ \begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \end{array} \right] $

The matrix only has 2 independent variables, therefore, the span is only defined for $\mathbb{R}^2$ and not all of $\mathbb{R}^3$.

---

1. Find the slope of the secant line between the value $a$ and $b$ for the following functions

a) $f(x) = (x − 2)^2, a = 2$ and $b = 3$

The slope of the secant line between $a$ and $b$ can be expressed as:
$\frac{f(b) - f(a)}{b - a}$

$f(a) = (a − 2)^2 = (2 - 2)^2 = 0^2 = 0$
$f(b) = (b − 2)^2 = (3 - 2)^2 = 1^2 = 1$

$\frac{f(b) - f(a)}{b - a} = \frac{1 - 0}{3 - 2} = \frac{1}{1} = 1$

$\therefore$ the slope of the secant line is $1$

b) $g(x) = \frac{1}{x − 1}, a = \frac{1}{2}$ and $b = 0$

The slope of the secant line between $a$ and $b$ can be expressed as:
$\frac{f(a) - f(b)}{a - b}$

$g(a) = \frac{1}{x − 1} = \frac{1}{a − 1} = \frac{1}{\frac{1}{2} − 1} = - \frac{1}{\frac{1}{2}} = - 2$
$g(b) = \frac{1}{x − 1} = \frac{1}{b − 1} = \frac{1}{0 − 1} = - \frac{1}{1} = - 1$

$\frac{g(a) - g(b)}{a - b} = \frac{(-2) - (-1)}{\frac{1}{2} - 0} = \frac{(-1}{\frac{1}{2}} = -2$

$\therefore$ the slope of the secant line is $-2$

c) $h(x) = \sqrt{5x − 2}, a = 1$ and $b = 2$

The slope of the secant line between $a$ and $b$ can be expressed as:
$\frac{h(b) - h(a)}{b - a}$

$h(a) = \sqrt{5x − 2} = \sqrt{5a − 2} = \sqrt{5 − 2} = \sqrt{3}$ / $h(b) = \sqrt{5x − 2} = \sqrt{5b − 2} = \sqrt{5(2) − 2} = \sqrt{10 − 2} = \sqrt{8} = 2 \sqrt{2}$

$\frac{h(b) - h(a)}{b - a} = \frac{2 \sqrt{2} - \sqrt{3}}{2 - 1} = \frac{2 \sqrt{2} - \sqrt{3}}{1} = 2 \sqrt{2} - \sqrt{3}$

$\therefore$ the slope of the secant line is $2 \sqrt{2} - \sqrt{3}$ or $1.09638$

2. Using the definition of the derivative, find the derivative at value $a$ of the following functions

a) $f(x) = (x − 2)^2, a = 2$

First, Find the derivative of f:
$\lim\limits_{h \to 0} \frac{f(x + h) - f(x)}{h} = \frac{(x + h - 2)^2 - (x^2 - 2)^2}{h} = \frac{(x^2 + xh - 2x + xh + h^2 - 2h - 2x - 2h + 4) - (x^2 - 2x - 2x + 4)}{h}$
$= \lim\limits_{h \to 0} \frac{x^2 + xh - 2x + xh + h^2 - 2h - 2x - 2h + 4 - x^2 + 2x + 2x - 4}{h} = \frac{h^2 + 2xh - 4h}{h} = h + 2x - 4$
$ \Rightarrow 2x - 4$

$\therefore$ f’(x) = 2x - 4

Then substitute $a$ in for $x$:
$f’(a) = 2a - 4 = 2(2) - 4 = 0$

$\therefore f’(a) = 0$

b) $g(x) = \frac{1}{x − 1}, a = \frac{1}{2}$

First, Find the derivative of g:
$\lim\limits_{h \to 0} \frac{g(x + h) - g(x)}{h} = \frac{ \frac{1}{x + h - 1} - \frac{1}{x - 1}}{h} =\frac{ \frac{x - 1 - x - h + 1}{(x + h - 1)(x - 1)}}{h} = \frac{ \frac{x - 1 - x - h + 1}{x^2 + xh - x + h - x - h + 1}}{h} = \frac{ \frac{-h}{x^2 + xh - 2x + 1}}{h}$
$ \lim\limits_{h \to 0} \frac{-1}{x^2 + xh - 2x + 1} \Rightarrow - \frac{1}{x^2 - 2x + 1}$

$ \therefore g’(x)= - \frac{1}{x^2 - 2x + 1}$

Then substitute $a$ in for $x$:
$g’(a)= - \frac{1}{a^2 - 2a + 1} = - \frac{1}{\frac{1}{2}^2 - 2(\frac{1}{2}) + 1} = - \frac{1}{\frac{1}{2}^2} = - \frac{1}{\frac{1}{4}} = -4$

$\therefore g’(a) = -4$

c) $h(x) = \sqrt{5x − 2}, a = 1$

First, Find the derivative of h:
$\lim\limits_{h \to 0} \frac{h(x + h) - h(x)}{h}$ $ = \frac{\sqrt{5(x + h) - 2} - \sqrt{5x - 2}}{h}$
$ = \frac{\sqrt{5x + 5h - 2} - \sqrt{5x - 2}}{h}$
$ = \frac{\sqrt{5x + 5h - 2} - \sqrt{5x - 2}}{h} \cdot \frac{\sqrt{5x + 5h - 2} + \sqrt{5x - 2}}{\sqrt{5x + 5h - 2} + \sqrt{5x - 2}}$ $ = \frac{5x + 5h - 2 - (5x - 2)}{h(\sqrt{5x + 5h - 2} + \sqrt{5x - 2})}$
$ = \frac{5x + 5h - 2 - 5x + 2)}{h(\sqrt{5x + 5h - 2} + \sqrt{5x - 2})}$
$ = \frac{5h}{h(\sqrt{5x + 5h - 2} + \sqrt{5x - 2})}$
$ \Rightarrow \frac{5}{\sqrt{5x - 2} + \sqrt{5x - 2}}$
$ = \frac{5}{2\sqrt{5x - 2}}$

$\therefore h’(x) = \frac{5}{2\sqrt{5x - 2}}$

Then substitute $a$ in for $x$:
$h’(a) = \frac{5}{2\sqrt{5a - 2}} = \frac{5}{2\sqrt{5(1) - 2}}$
$ = \frac{5}{2\sqrt{5 - 2}}$
$ = \frac{5}{2\sqrt{3}}$

$\therefore h’(a) = \frac{5}{2\sqrt{3}}$

3. Find the equation of the tangent line at value a of the following functions

a) $f(x) = (x − 2)^2, a = 2$

First we use our derivate (the derivative gives us the tangent line for any value on the domain)
$f’(x) = 2x - 4$

Then we use the substituted x to a value from before as our slope
$f’(a) = 0$

Then we put a in the original equation to get y and solve with point slope form
$f(a) = (a − 2)^2 = (2 - 2)^2 = 0^2 = 0$

$\therefore$ the equation of the tangent line of f(a) is $ y - 0 = 0(x - 0)$ or $ y = 0$

b) $g(x) = \frac{1}{x − 1}, a = \frac{1}{2}$

First we use our derivate (the derivative gives us the tangent line for any value on the domain)
$g’(x)= - \frac{1}{x^2 - 2x + 1}$

Then we use the substituted x to a value from before as our slope
$ g’(a) = -4$

Then we put a in the original equation to get y and solve with point slope form
$g(a) = \frac{1}{a - 1} = \frac{1}{ \frac{1}{2} - 1} = \frac{1}{ - \frac{1}{2}} = -2$

$\therefore$ the equation of the tangent line of g(a) is $ y - (-2) = -4(x - \frac{1}{2})$ or $y = -4x$

c) $h(x) = \sqrt{5x − 2}, a = 1$

First, we use our derivative from earlier:
$h’(x) = \frac{5}{2\sqrt{5x - 2}}$

Then we use the substituted x to a value from before as our slope
$h’(a) = \frac{5}{2\sqrt{3}}$

Then we put a in the original equation to get y and solve with point slope form
$h(a) = \sqrt{5a - 2} = \sqrt{5(1) - 2} = \sqrt{3}$

$\therefore$ the equation of the tangent line of h(a) is $ y - \sqrt{3} = \frac{5}{2\sqrt{3}}(x - 1)$ or $ y = \frac{5}{2\sqrt{3}}x - \frac{5}{2\sqrt{3}} + \sqrt{3}$

4. For each of the following statement determine whether it is true or false. If it is true, give a proof. If it is false, give a counterexample.

a) If $f$ is continuous on $\mathbb{R}$, then $f$ is differentiable on $\mathbb{R}$.

This Statement is False

Counterexample: the absolute value function contradicts this statement

Consider that $f(x) = |x|$ is continuous for all of $\mathbb{R}$
and $f’(x) = \frac{x}{|x|}$. if x = 0, then $f(0)$ would not be differentiable as that would lead to $\frac{0}{|0|}$.

$\therefore$ the statement is False

b) If $g$ is differentiable at $c$ and $f$ is not differentiable at $g(c)$, then $f ◦ g$ is not differentiable at $c$

This Statement is True

Proof: Chain Rule

When dealing with composite functions, the tool you always use is Chain rule. If Chain rule dose not work, then you cannot get the derivate of the function. In order for chain rule to work, you need g to be differentiable at c and f to be differentiable at g(c), as outlined in the rule’s definition: $(f \circ g)’(x) = f’(g(x)) \cdot g’(x)$. So if $f’g(c)$ dose not exist then $(f \circ g)’(x)$ cannot exist either, making $ f \circ g$ is not differentiable.

$\therefore$ the statement is True