CISC 102 - Day 8

2024-10-11 10:58:09 -0400 EDT

---

Methods

---

Principal of Exclusion and Delusion

Suppose $A_1$ and $A_2$ are sets, then:
$ | A_1 \cup A_2 | = | A_1 | + | A_2 | - | A_1 \cap A_2 |$ \

Note: absolute value of a set is the number of objects in the set

---

Pascals Triangle and Identity

$C(n, r)$ can be written as $ _nC_r$

We can create a triable where the top is $_0C_0$ and each row down increments $n$ and each column right increments $r$

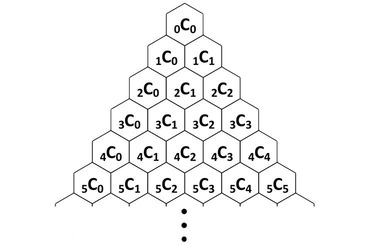
if you calculate each number, it could rewrite it as:

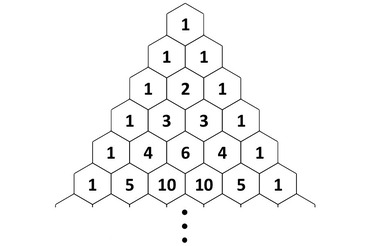
if look closely at the second image, you might notice that the sum of two numbers next to each other, is the number directly below them. which means

$ _nC_r = _NC_R + _NC_r $
$ N = n - 1$
$ R = r -1$

---

Lattice Paths

count the number of paths from origin $(0,0)$ to point $(m,n)$ when only moving towards $(m, n)$ You can do this by converting an up movement as a 1, and right movement as a 0, making each path a bit string.

notice that the amount of 1s or ups is equal to $n$, and the amount of 0s or rights is equal to $m$, meaning that total amount of bits in the string is equal to $m + n$. you can then interpret this question as the amount of ways you can arrange 1s in a bit string, making the equation

$ a = m + n$
$ _aC_n = \frac{(m + n)!}{n! m!}$

---

Anagrams

In linguists, an anagram is a word that can be created by with the letters of another word (i.e. listen is an anagram of silent). but in math, an anagram is any combination of letters from a word (i.e. estlni is anagram of silent). the amount of anagrams can be calculated with:

$ \frac{n!}{k_1! \cdot k_2! \cdot … \cdot k_m!}$
n = amount of letters in the word
k = amount of repeated letters
m = amount of times there is repeated letters

For example: BALLOONS $= \frac{8!}{2! \cdot 2!} = 10080$

Note: if you require to letters to be next to each other, you treat them as one letter (i.e. balloons become [BA, L, L, O, O, N, S]). if you require them to be separate, you calculate the amount of combinations of them together, and subtract that form the normal condition

Note: Spaces do not count as characters, and capital letters are different from.

---

Stars and Bars

Finds the amount of indistinguishable objects in distinguishable bins

we can visualize this stars (*) as the objects and bars (|) as the bins (i can’t really visualize this in markdown since asterisks are used for italicizing but trust me it works)

the equation for this relationship can be expressed with:
n = sum of stars
k = sum of bars
$ a = k - 1$
$ b = n + k - 1$
$ _bC_a = \frac{(n + k - 1)!}{n!(k - 1)!}$

Example: Six balls in 4 bags
$\frac{(6 + 4 - 1)!}{6!(4 - 1)!} = \frac{9!}{6! 3!}$

Note: if every bar requires a star, then you get subtract the amount of bars from stars

If you require one bar must have no stars, then we subtract it by the negation of the statement (all bars must have one star)