MATH 120 - Day 10

2024-10-14 19:47:25 -0400 EDT

---

Inverse Functions

Definition: if $f$ and $g$ are inverse of each other, then $f(g(x)) = x$ and $g(f(x)) = x$. We denote this as $g = f^{-1}$ and $f = g^{-1}$

Note: domain(f) = range(f^{-1})

I way to visualize inverse functions is to flip it the function across the diagonal (also known as the identity function)

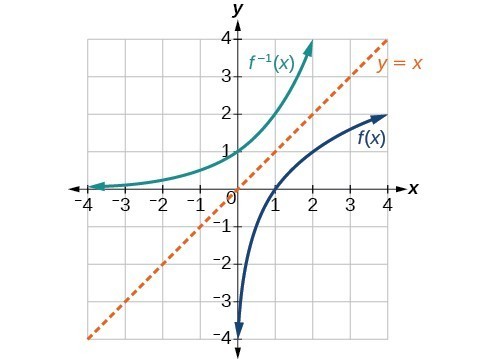
this also means you not all functions are not ineversible (some functions flipped on this axis will become relations instead of function). to test if a function is ineversible, you check if the function passes the same y value more then once (also know as the Horizontal Line Test).

then you could say that a function is ineversible if it is always increasing or decreasing, a Monotone function.

---

Derivate of Inverse Functions

if $f$ is differentiable at $a$ and $f’(a) = 0$, then $f^{-1}$ is differentiable at $f(a)$ and:
$(f^{-1})’(f(a)) = \frac{1}{f(a)}$

However! if $f’(a) \neq 0$, then $(f^{-1})’(f(a)) = \frac{1}{f’(f^{-1}(a))}$

Note: $f(x) = ln(x) \Rightarrow f’(x) = - \frac{1}{x}

Note: $x^{\alpha} = e^{\alpha ln(x)}, \alpha \in \mathbb{R}$