MATH 120 - Day 7

2024-09-18 21:27:42 -0400 EDT

One sided limits

Examples:

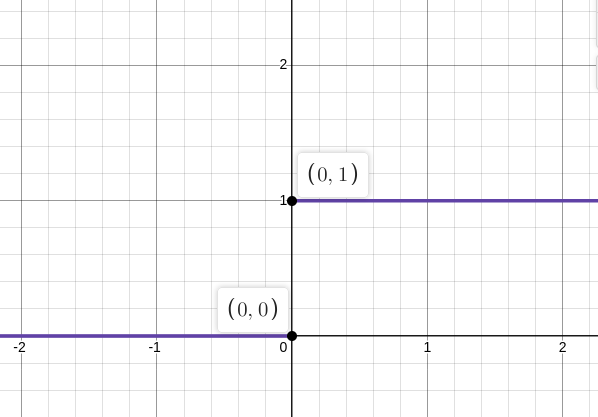
graph

$ f(x) = \left( \begin{array}{rrrrrr} 1 \text{ for } x \geq 0 \\ 0 \text{ for } x \le 0 \end{array} \right) $

$ \lim\limits_{x \to 0^+} f(x) = 1 $
$ x \to 0^+ :=$ from the right side of the graph

Real Definition of a limit

$$ \lim\limits_{x \to c} f(x) = L := \forall \epsilon > 0, \exists \delta > 0, , | x - c | < \delta \Rightarrow | f(x) - L | < \epsilon$$

Example: $ \lim\limits_(x \to 0) \sqrt{x} = 0$, prove with $\epsilon - \delta$

pick a $\epsilon, \epsilon > 0$. Find $\delta < 0$ such that if $ | v - c | =x < \delta$ then $ | f(x) - L | < \epsilon> $

$\sqrt{x} < \epsilon \Leftrightarrow (\sqrt{x})^2 < \epsilon^2 \Leftrightarrow x < \epsilon^2 \Rightarrow \sqrt{x} < 3. \therefore \delta = \epsilon ^2 > 0$

Example: $ \lim\limits_{x \to c} ( f(x) + g(x)) = \lim\limits_{ x \to 0} = \lim\limits_{x \to 0} f(x) + \lim\limits_{x \to 0} g(x) $

Let $ \lim\limits_{x \to c} f(x) = L_1, \lim\limits_{x \to c} g(x) = L_2, L = L_1 + L_2 \epsilon > 0 $
$ | f(x) + g(x) - L | = | (f(x) - L_1) + (g(x) - L_2) | \leq | f(x) - L_1 | + |g(x) - L_2 | < \epsilon \ \ $ ???

$ \lim\limits_{x \to c} f(x) = L_1 by \epsilon, \delta$ such that $ | x - c | < d_1 \Rightarrow | f(x) - L_1 | | x - c | < min(d_1, d_2) = d > 0 \Rightarrow | (f(x) + g(x)) - L | < \epsilon$